Question

5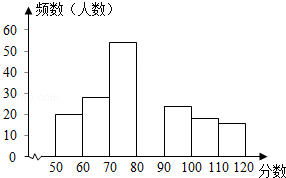．某课题组为了解全市九年级学生对数学知识的掌握情况，在一次数学检测中，从全市20000名九年级考生中随机抽取部分学生的数学成绩进行调查，并将调查结果绘制成如图表：

分数段	频数	频率
50≤x＜60	20	0.10
60≤x＜70	28	b
70≤x＜80	54	0.27
80≤x＜90	a	0.20
90≤x＜100	24	0.12
100≤x＜110	18	0.09
110≤x＜120	16	0.08

（1）表中a和b所表示的数分别为：a=40，b=0.14；
（2）请在图中补全频数分布直方图；
（3）如果把成绩在70分及以上定为合格，那么该市20000名九年级考生数学成绩为合格的学生约有多少名？
（4）若从调查部分的学生中随机抽取一名学生，则抽到成绩位于100≤x＜110的概率是多少？

Answer 1

分析 （1）可先求出抽查的人数，根据50≤x＜60这个分数段可求出抽查的人数为：20÷0.10=200人，根据频率=$\frac{频数}{抽查的数}$，可求出a和b的值．
（2）根据（1）求出的a的值，画在图上就可以．
（3）由70分以上频率和×20000，即可求出该市20000名九年级考生数学成绩为合格的学生人数．
（4）样本容量为200，由频数分布直方图可知，成绩成绩位于100≤x＜110的有18人，用频数除以样本容量即可求得其频率．

解答 解：（1）抽查人数：20÷0.10=200（人），
则a=200×0.20=40（人），
b=$\frac{28}{200}$=0.14．
故答案为40，0.14．
（2）补全频数分布直方图，如图：

（3）20000×（0.27+0.20+0.12+0.09+0.08）=15200（人）．
答：该市20000名九年级考生数学成绩为合格的学生约有15200人．
（4）抽到成绩位于100≤x＜110的概率=$\frac{18}{200}$=$\frac{9}{100}$．

点评 本题考查频数分布直方图，从图上获得信息的能力．熟悉掌握频率=$\frac{频数}{总数}$是解题关键．