题目内容
14.问题情境:一个三位数,它的十位上的数字比百位上的数字的3倍大1,个位上的数字是百位上的数字的3倍,现把这个三位数的百位上的数字和个位上的数字对调,得到一个新的三位数.尝试解决:
(1)设百位上的数字为x,则十位上的数字可表示为3x+1,个位上的数字可表示为3x.
(2)原三位数可表示为100•x+10(3x+1)+3x,化简,得133x+10(化简要有过程).
(3)新三位数可表示为100•3x+10•(3x+1)+x,化简,得331x+10(化简要有过程).
合作交流:
(4)求新三位数与原三位数的差,看看这个差有什么特点,写出一条来.
分析 (1)利用十位上的数字比百位上的数字的3倍大1,个位上的数字是百位上的数字的3倍可分别表示出十位上的数字和个位上的数字;
(2)分别把百位上的数字乘以100,十位上的数字乘以10后相加,然后再加上个位数字即可得到原三位数;
(3)与(2)的求解方法一样;
(4)先求两数的差,然后写出一条关于差的特点即可.
解答 解:(1)设百位上的数字为x,则十位上的数字可表示为3x+1,个位上的数字可表示为3x;
(2)原三位数可表示为100•x+10(3x+1)+3x,
100•x+10(3x+1)+3x=100x+30x+10+3x=133x+10;
(3)新三位数可表示为100•3x+10•(3x+1)+x,
100•3x+10•(3x+1)+x=300x+30x+10+x=331x+10;
(3)331x+10-(133x+10)=198x,
新三位数与原三位数的差等于新三位数的百位数字与个位数字差的99倍.
故答案为:3x+1,3x;100•x+10(3x+1)+3x,133x+10;100•3x+10•(3x+1)+x,331x+10.
点评 本题考查了列代数式:把问题中与数量有关的词语,用含有数字、字母和运算符号的式子表示出来,就是列代数式. 列代数式时,要先认真审题,抓住关键词语,仔细辩析词义;分清数量关系;规范书写格式.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
5.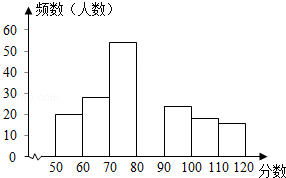 某课题组为了解全市九年级学生对数学知识的掌握情况,在一次数学检测中,从全市20000名九年级考生中随机抽取部分学生的数学成绩进行调查,并将调查结果绘制成如图表:
某课题组为了解全市九年级学生对数学知识的掌握情况,在一次数学检测中,从全市20000名九年级考生中随机抽取部分学生的数学成绩进行调查,并将调查结果绘制成如图表:
(1)表中a和b所表示的数分别为:a=40,b=0.14;
(2)请在图中补全频数分布直方图;
(3)如果把成绩在70分及以上定为合格,那么该市20000名九年级考生数学成绩为合格的学生约有多少名?
(4)若从调查部分的学生中随机抽取一名学生,则抽到成绩位于100≤x<110的概率是多少?
 某课题组为了解全市九年级学生对数学知识的掌握情况,在一次数学检测中,从全市20000名九年级考生中随机抽取部分学生的数学成绩进行调查,并将调查结果绘制成如图表:
某课题组为了解全市九年级学生对数学知识的掌握情况,在一次数学检测中,从全市20000名九年级考生中随机抽取部分学生的数学成绩进行调查,并将调查结果绘制成如图表:| 分数段 | 频数 | 频率 |
| 50≤x<60 | 20 | 0.10 |
| 60≤x<70 | 28 | b |
| 70≤x<80 | 54 | 0.27 |
| 80≤x<90 | a | 0.20 |
| 90≤x<100 | 24 | 0.12 |
| 100≤x<110 | 18 | 0.09 |
| 110≤x<120 | 16 | 0.08 |
(2)请在图中补全频数分布直方图;
(3)如果把成绩在70分及以上定为合格,那么该市20000名九年级考生数学成绩为合格的学生约有多少名?
(4)若从调查部分的学生中随机抽取一名学生,则抽到成绩位于100≤x<110的概率是多少?
 如图,AB是⊙O的直径,∠E=25°,∠DBC=45°,则∠CBE=55°.
如图,AB是⊙O的直径,∠E=25°,∠DBC=45°,则∠CBE=55°.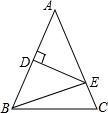 如图,在△ABC中,AC=12cm,ED垂直平分AB,如果△EBC的周长是20cm,那么BC的长度为8cm.
如图,在△ABC中,AC=12cm,ED垂直平分AB,如果△EBC的周长是20cm,那么BC的长度为8cm.