题目内容
13．若关于x的方程x2+x-a+$\frac{9}{4}$=0没有实数根，则实数a的取值范围是（ ）| A． | a≥2 | B． | a≤2 | C． | a＜2 | D． | a＞2 |
分析 根据判别式的意义得到△=12-4（-a+$\frac{9}{4}$）＜0，然后解不等式即可．
解答 解：∵关于x的方程x2+x-a+$\frac{9}{4}$=0没有实数根，
∴△=12-4（-a+$\frac{9}{4}$）＜0，
解得：a＜2，
故选C．
点评 本题考查了一元二次方程ax2+bx+c=0（a≠0）的根的判别式△=b2-4ac：当△＞0，方程有两个不相等的实数根；当△=0，方程有两个相等的实数根；当△＜0，方程没有实数根．
练习册系列答案
培优好卷单元加期末卷系列答案
相关题目
如图，AB是⊙O的直径，∠E=25°，∠DBC=45°，则∠CBE=55°．
5．
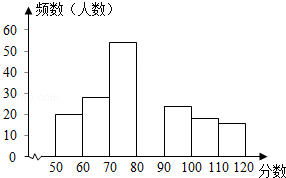某课题组为了解全市九年级学生对数学知识的掌握情况，在一次数学检测中，从全市20000名九年级考生中随机抽取部分学生的数学成绩进行调查，并将调查结果绘制成如图表：
（1）表中a和b所表示的数分别为：a=40，b=0.14；
（2）请在图中补全频数分布直方图；
（3）如果把成绩在70分及以上定为合格，那么该市20000名九年级考生数学成绩为合格的学生约有多少名？
（4）若从调查部分的学生中随机抽取一名学生，则抽到成绩位于100≤x＜110的概率是多少？
某课题组为了解全市九年级学生对数学知识的掌握情况，在一次数学检测中，从全市20000名九年级考生中随机抽取部分学生的数学成绩进行调查，并将调查结果绘制成如图表：| 分数段 | 频数 | 频率 |
| 50≤x＜60 | 20 | 0.10 |
| 60≤x＜70 | 28 | b |
| 70≤x＜80 | 54 | 0.27 |
| 80≤x＜90 | a | 0.20 |
| 90≤x＜100 | 24 | 0.12 |
| 100≤x＜110 | 18 | 0.09 |
| 110≤x＜120 | 16 | 0.08 |
（2）请在图中补全频数分布直方图；
（3）如果把成绩在70分及以上定为合格，那么该市20000名九年级考生数学成绩为合格的学生约有多少名？
（4）若从调查部分的学生中随机抽取一名学生，则抽到成绩位于100≤x＜110的概率是多少？