题目内容
19．
如图，△ABC以点O为旋转中心，旋转180°后得到△A′B′C′．ED是△ABC的中位线，经旋转后为线段E′D′．已知BC=8，则E′D′=4．
分析 先根据三角形中位线性质得ED=4，然后根据旋转的性质求解．
解答 解：∵ED是△ABC的中位线，
∴ED=$\frac{1}{2}$BC=4，
∵△ABC以点O为旋转中心，旋转180°后得到△A′B′C′．ED经旋转后为线段E′D′，
∴D′E′=DE=4．
故答案为4．
点评 本题考查了旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．也考查了三角形中位线性质．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
10．在0，-1，-2，-3，-$\frac{10}{3}$中，最小的数是（ ）
| A． | 0 | B． | -1 | C． | -$\frac{10}{3}$ | D． | -3 |
14．下列算式中，正确的是（ ）
| A． | $-{a^2}÷a•\frac{1}{a}=-{a^2}$ | B． | （a+2）2=a2+4 | C． | -（-a3）2=a6 | D． | （-a3b）2=a6b2 |
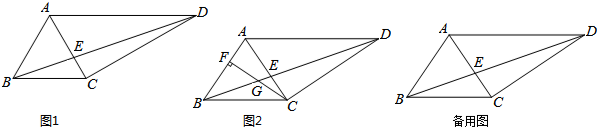
如图，在矩形ABCD中，点O是AC的中点，AC=2AB，延长AB至G，使BG=AB，连接GO交BC于点E，延长GO交AD于点F，判断四边形AECF的形状，并证明你的结论．