题目内容
4.已知抛物线y=3x2+1与直线y=4sinα•x只有一个交点,则锐角α等于( )| A. | 60° | B. | 45° | C. | 30° | D. | 15° |
分析 抛物线y=3x2+1与直线y=4sinα•x只有一个交点,则把y=4sinα•x代入二次函数的解析式,得到的关于x的方程中,判别式△=0,据此即可求解.
解答 解:根据题意得:3x2+1=4sinα•x,
即3x2-4sinαx+1=0,
则△=16sin2α-4×3×1=0,
解得:sinα=$\frac{\sqrt{3}}{2}$,
所以α=60°.
故选A.
点评 本题考查了二次函数与一次函数的交点个数的判断,把一次函数代入二次函数的解析式,得到的关于x的方程中,判别式△>0,则两个函数有两个交点,若△=0,则只有一个交点,若△<0,则没有交点,也考查了直角三角函数.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.正方形的正投影不可能是( )
| A. | 正方形 | B. | 长方形 | C. | 线段 | D. | 梯形 |

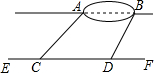 小明想测量位于池塘两端的A、B两点的距离.他沿着与直线AB平行的道路EF行走,当行走到点C处,测得∠ACF=45°,再向前行走100米到点D处,测得∠BDF=60°.若直线AB与EF之间的距离为60米,求A、B两点的距离(结果保留根号).
小明想测量位于池塘两端的A、B两点的距离.他沿着与直线AB平行的道路EF行走,当行走到点C处,测得∠ACF=45°,再向前行走100米到点D处,测得∠BDF=60°.若直线AB与EF之间的距离为60米,求A、B两点的距离(结果保留根号).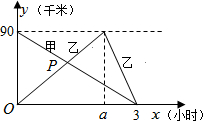 在一条笔直的公路上有A、B两地,甲从A地去B地,乙从B地去A地然后立即原路返回B地,返回时的速度是原来的2倍,如图是甲、乙两人离B地的距离y(千米)和时间x(小时)之间的函数图象.请根据图象回答下列问题:
在一条笔直的公路上有A、B两地,甲从A地去B地,乙从B地去A地然后立即原路返回B地,返回时的速度是原来的2倍,如图是甲、乙两人离B地的距离y(千米)和时间x(小时)之间的函数图象.请根据图象回答下列问题:
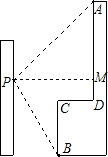 小明在教学楼的点P处观测对面的实验楼,为了测量坐在位置点P到对面实验楼上部AD的距离,小强测得实验楼楼顶部点A的仰角为45°,测得实验楼底部点B的俯角为60°,已知实验楼高30米,CD=10米.求点P到AD的距离(结果保留到0.1米)
小明在教学楼的点P处观测对面的实验楼,为了测量坐在位置点P到对面实验楼上部AD的距离,小强测得实验楼楼顶部点A的仰角为45°,测得实验楼底部点B的俯角为60°,已知实验楼高30米,CD=10米.求点P到AD的距离(结果保留到0.1米)