题目内容
16.如图①、②、③是三个可以自由转动的转盘.(1)若同时转动①、②两个转盘,则两个转盘停下时指针所指的数字都是2的概率为$\frac{1}{4}$;
(2)甲、乙两人用三个转盘玩游戏,甲转动转盘,乙记录指针停下时所指的数字.游戏规定:当指针所指的三个数字中有数字相同时,就算甲赢,否则就算乙赢.请判断这个游戏是否公平,并说明你的理由.

分析 (1)画出树状图,根据概率公式计算即可;
(2)画出树状图,计算出各种情况的概率,然后比较即可.相等则公平,否则不公平
解答 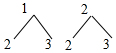 解:(1)画树状图,
解:(1)画树状图,
共有4个可能的结果,两个转盘停下时指针所指的数字都是2的结果有1个,
∴P(两个转盘停下时指针所指的数字都是2)=$\frac{1}{4}$;
故答案为$\frac{1}{4}$;
(2)不公平,理由如下:
画树状图如下: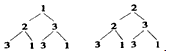 由图可知:共有8种结果,且是等可能的,其中含有相同数字的结果有6种.
由图可知:共有8种结果,且是等可能的,其中含有相同数字的结果有6种.
因此甲获胜的概率=$\frac{6}{8}$=$\frac{3}{4}$,乙获胜的概率=$\frac{2}{8}$=$\frac{1}{4}$,所以这个游戏不公平.
点评 本题考查的是游戏公平性的判断、列表法与树状图法.判断游戏公平性就要计算每个参与者取胜的概率,概率相等就公平,否则就不公平.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
6.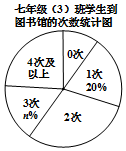 为了落实漳州市教育局关于全市中小学生每天阅读1小时的文件精神.某校对七年级(3)班全体学生一周到图书馆的次数做了调查统计,以下是调查过程中绘制的还不完整的两个统计图.请你根据统计图表中的信息,解答下列问题:
为了落实漳州市教育局关于全市中小学生每天阅读1小时的文件精神.某校对七年级(3)班全体学生一周到图书馆的次数做了调查统计,以下是调查过程中绘制的还不完整的两个统计图.请你根据统计图表中的信息,解答下列问题:
(1)求图表中m,n的值;
(2)该年级学生共有300人,估计这周到图书馆的次数为“4次及以上”的学生大约有多少人?
七年级(3)班学生到图书馆的次数统计表
 为了落实漳州市教育局关于全市中小学生每天阅读1小时的文件精神.某校对七年级(3)班全体学生一周到图书馆的次数做了调查统计,以下是调查过程中绘制的还不完整的两个统计图.请你根据统计图表中的信息,解答下列问题:
为了落实漳州市教育局关于全市中小学生每天阅读1小时的文件精神.某校对七年级(3)班全体学生一周到图书馆的次数做了调查统计,以下是调查过程中绘制的还不完整的两个统计图.请你根据统计图表中的信息,解答下列问题:(1)求图表中m,n的值;
(2)该年级学生共有300人,估计这周到图书馆的次数为“4次及以上”的学生大约有多少人?
七年级(3)班学生到图书馆的次数统计表
| 到图书馆的 次数 | 0次 | 1次 | 2次 | 3次 | 4次及 以上 |
| 人数 | 5 | 10 | m | 8 | 12 |
4.已知抛物线y=3x2+1与直线y=4sinα•x只有一个交点,则锐角α等于( )
| A. | 60° | B. | 45° | C. | 30° | D. | 15° |
6.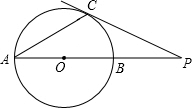 如图,已知⊙O的直径AB与弦AC的夹角为30°,过C点的切线PC与AB的延长线于P.若圆半径等于5,则线段CP的长度是( )
如图,已知⊙O的直径AB与弦AC的夹角为30°,过C点的切线PC与AB的延长线于P.若圆半径等于5,则线段CP的长度是( )
 如图,已知⊙O的直径AB与弦AC的夹角为30°,过C点的切线PC与AB的延长线于P.若圆半径等于5,则线段CP的长度是( )
如图,已知⊙O的直径AB与弦AC的夹角为30°,过C点的切线PC与AB的延长线于P.若圆半径等于5,则线段CP的长度是( )| A. | 5$\sqrt{3}$ | B. | 5 | C. | 10 | D. | $\frac{5\sqrt{3}}{3}$ |
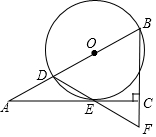 如图,在Rt△ABC中,∠ACB=90°,∠A=30°,点D在AB上,以BD为直径的⊙O切AC于点E,连接DE并延长,交BC的延长线于点F.
如图,在Rt△ABC中,∠ACB=90°,∠A=30°,点D在AB上,以BD为直径的⊙O切AC于点E,连接DE并延长,交BC的延长线于点F. 如图,在边长相同的小正方形网格中,点A、B、C、D都在这些小正方形的顶点上,AB与CD相交于点P,则tan∠APD的值为2.
如图,在边长相同的小正方形网格中,点A、B、C、D都在这些小正方形的顶点上,AB与CD相交于点P,则tan∠APD的值为2.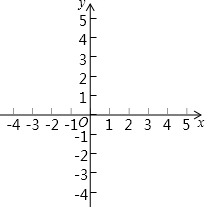 在平面直角坐标系xOy,直线y=x-1与y轴交于点A,与双曲线y=$\frac{k}{x}$交于点B(m,2)
在平面直角坐标系xOy,直线y=x-1与y轴交于点A,与双曲线y=$\frac{k}{x}$交于点B(m,2)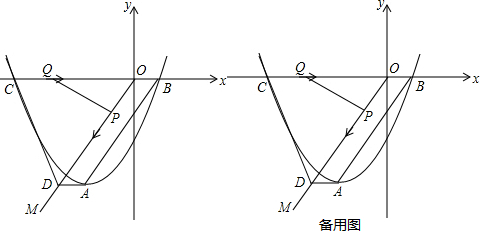
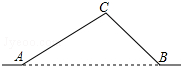 如图,从A地到B地的公路需要经过C地,根据规划,将在A,B两地之间修建一条笔直的公路.已知AC=10千米,∠CAB=34°,∠CBA=45°,求改直后公路AB的长(结果精确到0.1千米)
如图,从A地到B地的公路需要经过C地,根据规划,将在A,B两地之间修建一条笔直的公路.已知AC=10千米,∠CAB=34°,∠CBA=45°,求改直后公路AB的长(结果精确到0.1千米)