题目内容
12.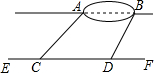 小明想测量位于池塘两端的A、B两点的距离.他沿着与直线AB平行的道路EF行走,当行走到点C处,测得∠ACF=45°,再向前行走100米到点D处,测得∠BDF=60°.若直线AB与EF之间的距离为60米,求A、B两点的距离(结果保留根号).
小明想测量位于池塘两端的A、B两点的距离.他沿着与直线AB平行的道路EF行走,当行走到点C处,测得∠ACF=45°,再向前行走100米到点D处,测得∠BDF=60°.若直线AB与EF之间的距离为60米,求A、B两点的距离(结果保留根号).
分析 作AM⊥EF于点M,作BN⊥EF于点N,可以分别求得CM、DN的长,由于AB=CN-CM,从而可以求得AB的长.
解答 解:作AM⊥EF于点M,作BN⊥EF于点N,如右图所示,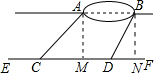
由题意可得,AM=BN=60米,CD=100米,∠ACF=45°,∠BDF=60°,
∴CM=$\frac{AM}{tan45°}$=$\frac{60}{1}$=60米,
DN=$\frac{BN}{tan60°}$=$\frac{60}{\sqrt{3}}$=20 $\sqrt{3}$米,
∴AB=CD+DN-CM=100+20 $\sqrt{3}$-60=(40+20 $\sqrt{3}$)米,
即A、B两点的距离是(40+20 $\sqrt{3}$)米.
点评 本题考查解直角三角形的应用,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考常考题型.

练习册系列答案
相关题目
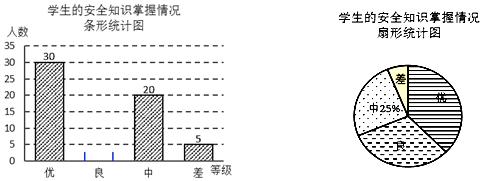
20.某校兴趣小组对网上吐糟较为频繁的“医患关系”产生了兴趣,利用节假日在某社区开展了“造成医患关系紧张的原因”的问卷调查.
根据调查结果绘制出了如下两幅尚不完整的统计图.
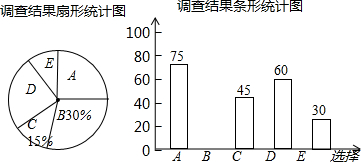
根据以上信息解答下列问题:
(1)这次接受调查的总人数为300人;
(2)在扇形统计图中,“A”所在扇形的圆心角的度数为90°;
(3)补全条形统计图;
(4)若该市有1000万人,请你估计选D的总人数.
| 造成医患关系紧张的原因(单选) A.药价高 B.检测项目太多且收费太高 C.住院报销比例低 D.医疗费与个人收入不相称 E.其他 |

根据以上信息解答下列问题:
(1)这次接受调查的总人数为300人;
(2)在扇形统计图中,“A”所在扇形的圆心角的度数为90°;
(3)补全条形统计图;
(4)若该市有1000万人,请你估计选D的总人数.
17. 某校1200名学生参加了全市组织的“经典诵读”活动,该校随机选取部分学生,对他们在三、四两个月的诵读时间进行调查,下面是根据调查数据制作的统计图表的一部分,三月日人均诵读时间的频数分布直方图.
某校1200名学生参加了全市组织的“经典诵读”活动,该校随机选取部分学生,对他们在三、四两个月的诵读时间进行调查,下面是根据调查数据制作的统计图表的一部分,三月日人均诵读时间的频数分布直方图.
根据以上信息,解答下列问题:
(1)本次调查的学生数为100人;
(2)图表中的a、b、c的值分别为6,4,4%;
(3)在被调查的学生中,四月份日人均诵读时间在1<x≤1.5范围内的人数比三月份在此范围的人数多44人;
(4)试估计该校学生四月份人均诵读时间在1小时以上的人数.
四月日人均诵读时间的统计表
 某校1200名学生参加了全市组织的“经典诵读”活动,该校随机选取部分学生,对他们在三、四两个月的诵读时间进行调查,下面是根据调查数据制作的统计图表的一部分,三月日人均诵读时间的频数分布直方图.
某校1200名学生参加了全市组织的“经典诵读”活动,该校随机选取部分学生,对他们在三、四两个月的诵读时间进行调查,下面是根据调查数据制作的统计图表的一部分,三月日人均诵读时间的频数分布直方图.根据以上信息,解答下列问题:
(1)本次调查的学生数为100人;
(2)图表中的a、b、c的值分别为6,4,4%;
(3)在被调查的学生中,四月份日人均诵读时间在1<x≤1.5范围内的人数比三月份在此范围的人数多44人;
(4)试估计该校学生四月份人均诵读时间在1小时以上的人数.
四月日人均诵读时间的统计表
| 日人均诵读时间x/h | 人数 | 百分比 |
| 0≤x≤0.5 | 6 | |
| 0.5<x≤1 | 30 | |
| 1<x≤1.5 | 50% | |
| 1.5<x≤2 | 10 | 10% |
| 2<x≤2.5 | b | c |
4.已知抛物线y=3x2+1与直线y=4sinα•x只有一个交点,则锐角α等于( )
| A. | 60° | B. | 45° | C. | 30° | D. | 15° |
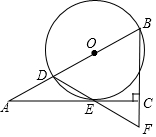 如图,在Rt△ABC中,∠ACB=90°,∠A=30°,点D在AB上,以BD为直径的⊙O切AC于点E,连接DE并延长,交BC的延长线于点F.
如图,在Rt△ABC中,∠ACB=90°,∠A=30°,点D在AB上,以BD为直径的⊙O切AC于点E,连接DE并延长,交BC的延长线于点F. 在平面直角坐标系xOy,直线y=x-1与y轴交于点A,与双曲线y=$\frac{k}{x}$交于点B(m,2)
在平面直角坐标系xOy,直线y=x-1与y轴交于点A,与双曲线y=$\frac{k}{x}$交于点B(m,2)