题目内容
13.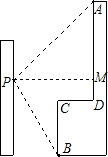 小明在教学楼的点P处观测对面的实验楼,为了测量坐在位置点P到对面实验楼上部AD的距离,小强测得实验楼楼顶部点A的仰角为45°,测得实验楼底部点B的俯角为60°,已知实验楼高30米,CD=10米.求点P到AD的距离(结果保留到0.1米)
小明在教学楼的点P处观测对面的实验楼,为了测量坐在位置点P到对面实验楼上部AD的距离,小强测得实验楼楼顶部点A的仰角为45°,测得实验楼底部点B的俯角为60°,已知实验楼高30米,CD=10米.求点P到AD的距离(结果保留到0.1米)
分析 连接PA、PB,过点P作PM⊥AD于点M;延长BC,交PM于点N,将实际问题中的已知量转化为直角三角形中的有关量,设PM=x米,在Rt△PMA中,表示出AM,在Rt△PNB中,表示出BN,由AM+BN=46米列出方程求解即可.
解答  解:连接PA、PB,过点P作PM⊥AD于点M;延长BC,交PM于点N
解:连接PA、PB,过点P作PM⊥AD于点M;延长BC,交PM于点N
则∠APM=45°,∠BPM=60°,NM=10米
设PM=x米
在Rt△PMA中,AM=PM×tan∠APM=xtan45°=x(米)
在Rt△PNB中,BN=PN×tan∠BPM=(x-10)tan60°=$\sqrt{3}$(x-10)(米)
由AM+BN=30米,得x+$\sqrt{3}$(x-10)=30
解得,x=10$\sqrt{3}$
∴点P到AD的距离为10$\sqrt{3}$米.
点评 此题考查了解直角三角形的知识,作出辅助线,构造直角三角形是解题的关键.

练习册系列答案
相关题目
4.已知抛物线y=3x2+1与直线y=4sinα•x只有一个交点,则锐角α等于( )
| A. | 60° | B. | 45° | C. | 30° | D. | 15° |
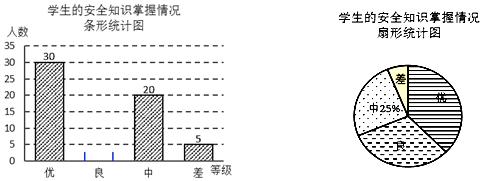
3.今年我市2017年初中毕业生学业考试10门学科整合后的满分值如表:
请问数据120,120,120,150,150,50,20,20中,众数、中位数分别是( )
| 科目 | 语文 | 数学 | 英语 | 理化生 | 政史地 | 体育 | 信息技术 | 实验操作 |
| 满分值 | 120 | 120 | 120 | 150 | 150 | 50 | 20 | 20 |
| A. | 150,120 | B. | 120,120 | C. | 130,120 | D. | 120,100 |
 在平面直角坐标系xOy,直线y=x-1与y轴交于点A,与双曲线y=$\frac{k}{x}$交于点B(m,2)
在平面直角坐标系xOy,直线y=x-1与y轴交于点A,与双曲线y=$\frac{k}{x}$交于点B(m,2)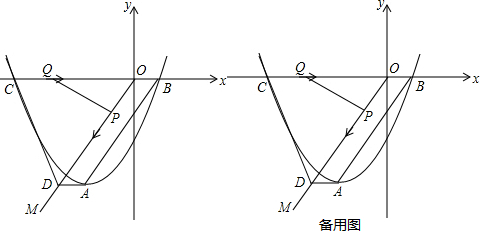
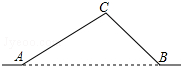 如图,从A地到B地的公路需要经过C地,根据规划,将在A,B两地之间修建一条笔直的公路.已知AC=10千米,∠CAB=34°,∠CBA=45°,求改直后公路AB的长(结果精确到0.1千米)
如图,从A地到B地的公路需要经过C地,根据规划,将在A,B两地之间修建一条笔直的公路.已知AC=10千米,∠CAB=34°,∠CBA=45°,求改直后公路AB的长(结果精确到0.1千米)