题目内容
6.找规律.1+3=4=22
1+3+5=9=32
1+3+5+7=16=42
1+3+5+7+9=25=52
(1)根据规律填空:1+3+5+7+9+11=36=62;
(2)根据规律计算:1+3+5+7+9+…+99.
分析 (1)根据有理数的加法法则计算即可;
(2)根据数字变化规律解答.
解答 解:(1)1+3+5+7+9+11
=36
=62,
故答案为:36;62;
(2)1+3+5+7+9+…+99
=($\frac{1+99}{2}$)2
=502
=2500.
点评 本题考查的是数字的变化规律,根据数字变换情况找出规律是解题的关键.

练习册系列答案
相关题目
17.因为cos60°=$\frac{1}{2}$,cos240°=-$\frac{1}{2}$,所以cos240°=cos(180°+60°)=-cos60°;由此猜想、推理知:当α为锐角时有cos(180°+α)=-cosα,由此可知:cos210°=( )
| A. | -$\frac{1}{2}$ | B. | -$\frac{\sqrt{2}}{2}$ | C. | -$\frac{\sqrt{3}}{2}$ | D. | -$\sqrt{3}$ |
14.发现思考:已知等腰三角形ABC的两边分别是方程x2-7x+10=0的两个根,求等腰三角形ABC三条边的长各是多少?下边是涵涵同学的作业,老师说他的做法有错误,请你找出错误之处并说明错误原因.
涵涵的作业
探究应用:请解答以下问题:
已知等腰三角形ABC的两边是关于x的方程x2-mx+$\frac{m}{2}$-$\frac{1}{4}$=0的两个实数根.
(1)当m=2时,求△ABC的周长;
(2)当△ABC为等边三角形时,求m的值.
涵涵的作业
| 解:x2-7x+10=0 a=1 b=-7 c=10 ∵b2-4ac=9>0 ∴x=$\frac{-b±\sqrt{{b}^{2}-4ac}}{2a}$=$\frac{7+3}{2}$ ∴x1=5,x2=2 所以,当腰为5,底为2时,等腰三角形的三条边为5,5,2. 当腰为2,底为5时,等腰三角形的三条边为2,2,5. |
已知等腰三角形ABC的两边是关于x的方程x2-mx+$\frac{m}{2}$-$\frac{1}{4}$=0的两个实数根.
(1)当m=2时,求△ABC的周长;
(2)当△ABC为等边三角形时,求m的值.
11.在△ABC中,AB=AC,AD是BC边上的高,若AB=5cm,BC=6cm,则AD的长是( )
| A. | 3cm | B. | 4cm | C. | 5cm | D. | 6cm |
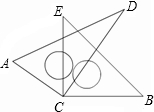 如图,将两块直角三角尺的直角顶点C叠放在一起.
如图,将两块直角三角尺的直角顶点C叠放在一起.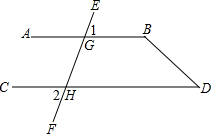 如图已知∠1=∠2,∠D=50°,
如图已知∠1=∠2,∠D=50°,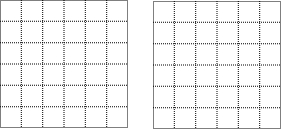 如图,正方形网络中的每个小正方形边长都为1,每个小正方形的顶点叫格点,分别按下列要求画以格点为顶点三角形和平行四边形.(无需写画法)
如图,正方形网络中的每个小正方形边长都为1,每个小正方形的顶点叫格点,分别按下列要求画以格点为顶点三角形和平行四边形.(无需写画法)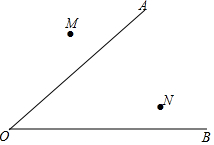 用直尺和圆规作图:(不写作法,保留作图痕迹)
用直尺和圆规作图:(不写作法,保留作图痕迹)