题目内容
甲、乙两车从A城出发前往B城．在整个行程中，汽车离开A城的距离y与时刻t的对应关系如图．（1）A，B两城相距多远？
（2）哪辆车先出发？哪辆车先到B城？
（3）甲、乙两车的平均速度分别是多少？
考点：一次函数的应用
专题：
分析：（1）根据图示知，纵坐标表示汽车离开A城的距离，所以A，B两城相距300米；
（2）根据甲、乙两车的出发时间和到达时间进行回答；
（3）速度=
，依此列式计算即可求解．
（2）根据甲、乙两车的出发时间和到达时间进行回答；
（3）速度=
| 距离 |
| 时间 |
解答：解：（1）由图示知：A，B两城相距300km；
（2）由图示知，甲车从5：00出发，乙车从6：00出发；甲车10：00到达B城，乙车9：00到达B城．
答：甲车先出发，乙车先到达B城；
（3）如图所示：甲车的平均速度为：
=60（km/h），
乙车的平均速度为：
=100（km/h），
答：甲、乙两车的平均速度分别是60km/h、100km/h．
（2）由图示知，甲车从5：00出发，乙车从6：00出发；甲车10：00到达B城，乙车9：00到达B城．
答：甲车先出发，乙车先到达B城；
（3）如图所示：甲车的平均速度为：
| 300 |
| 10-5 |
乙车的平均速度为：
| 300 |
| 9-6 |
答：甲、乙两车的平均速度分别是60km/h、100km/h．
点评：本题考查了一次函数的应用．主要利用了路程、速度、时间三者之间的关系，准确识图，理解横、纵坐标的实际意义是解题的关键．
练习册系列答案
相关题目
如图，能判断直线AB∥CD的条件是（ ）| A、∠3+∠4=180° |
| B、∠3=∠4 |
| C、∠1+∠3=180° |
| D、∠1=∠2 |
下列成语所描述的事件：
①水中捞月；②拔苗助长；③守株待兔；④瓮中捉鳖．
其中是确定事件的个数有（ ）
①水中捞月；②拔苗助长；③守株待兔；④瓮中捉鳖．
其中是确定事件的个数有（ ）
| A、1个 | B、2个 | C、3个 | D、4个 |
如图，平行四边形ABCD中，P是四边形内任意一点，△ABP，△BCP，△CDP，△ADP的面积分别为S1，S2，S3，S4，则一定成立的是（ ）| A、S1+S2＞S3+S4 |
| B、S1+S2=S3+S4 |
| C、S1+S2＜S3+S4 |
| D、S1+S3=S2+S4 |
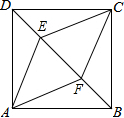如图，正方形ABCD中，点E、F为对角线BD上两点，DE=BF．
如图，△ABC与△CDE都是等边三角形，点E、F分别为AC、BC的中点．
如图，在△ABC中，AB=AC，∠B=60°，∠FAC、∠ECA是△ABC的两个外角，AD平分∠FAC，CD平分∠ECA．