题目内容
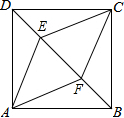 如图,正方形ABCD中,点E、F为对角线BD上两点,DE=BF.
如图,正方形ABCD中,点E、F为对角线BD上两点,DE=BF.①四边形AECF是什么四边形?并证明.
②若EF=4cm,DE=BF=2cm,求四边形AECF的周长.
考点:正方形的性质,勾股定理,菱形的判定与性质
专题:
分析:(1)连接AC,交BD于点O.利用正方形的性质得出AC⊥BD,OA=OC=OB=OD,进一步得出OE=OF,证得四边形AECF是菱形;
(2)利用菱形的性质和勾股定理求得即可.
(2)利用菱形的性质和勾股定理求得即可.
解答:解:连接AC,交BD于点O,

∵正方形ABCD,
∴AC⊥BD,OA=OC=OB=OD
∴DE=BF
∴OE=OF
∴四边形AECF是菱形.
(2)∵EF=4cm,DE=BF=2cm
∴AC=BD=8cm
∴AE=
=
=2
cm
∴四边形AECF的周长为8
cm.

∵正方形ABCD,
∴AC⊥BD,OA=OC=OB=OD
∴DE=BF
∴OE=OF
∴四边形AECF是菱形.
(2)∵EF=4cm,DE=BF=2cm
∴AC=BD=8cm
∴AE=
| OA2+OE2 |
| 42+22 |
| 5 |
∴四边形AECF的周长为8
| 5 |
点评:此题考查正方形的性质,菱形的判定,勾股定理等知识点,注意结合已知条件合理作出辅助线解决问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列各数,是最简二次的根的是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
下列的计算一定正确的是( )
| A、b3+b3=2b6 |
| B、(-3pq)2=-9p2q2 |
| C、(12a2b3c)÷(6ab2)=2ab |
| D、(x2-4x)x-1=x-4 |

 甲、乙两车从A城出发前往B城.在整个行程中,汽车离开A城的距离y与时刻t的对应关系如图.
甲、乙两车从A城出发前往B城.在整个行程中,汽车离开A城的距离y与时刻t的对应关系如图.

 如图,在平面直角坐标系中,菱形ABCD的顶点B、C的坐标分别为B(0,0),C(6,0),且∠B=60°.动点P、Q分别从点B、点D同时出发,点P以每秒2个单位的速度向点A移动;点Q以每秒3个单位的速度向点A移动.设两动点运动的时间为t秒,其中0<t<2.
如图,在平面直角坐标系中,菱形ABCD的顶点B、C的坐标分别为B(0,0),C(6,0),且∠B=60°.动点P、Q分别从点B、点D同时出发,点P以每秒2个单位的速度向点A移动;点Q以每秒3个单位的速度向点A移动.设两动点运动的时间为t秒,其中0<t<2.