题目内容
18. 如图,在平面直角坐标系中,⊙P与x轴相切于原点O,平行于y轴的直线交⊙P于E,F两点,若点E的坐标是(-3,-1),则点F的坐标是(-3,-9).
如图,在平面直角坐标系中,⊙P与x轴相切于原点O,平行于y轴的直线交⊙P于E,F两点,若点E的坐标是(-3,-1),则点F的坐标是(-3,-9).
分析 过点P作AP⊥EF交EF于点A,连接PE,设OP=x,由点E的坐标易求AP=OB=3,AE=AB-BE=x-1,在Rt△ABE中,由勾股定理可得32+(x-1)2=x2,解得x的值,即可求出BF的长,进而可求出点F的坐标.
解答 解:过点P作AP⊥EF交EF于点A,连接PE,设OP=x,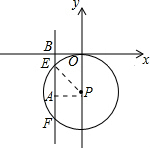
∵⊙P与x轴相切于原点O,
∴OP⊥OE,
∵平行于y轴的直线交⊙P于E,F两点,
∴四边形APOB是矩形,
∴AB=OP=x,
∵点E的坐标是(-3,-1),
∴AP=OB=3,AE=AB-BE=x-1,
在Rt△ABE中,32+(x-1)2=x2,
解得x=5,
∴AE=4,
∵AF=AE,
∴EF=8,
∴BF=EF+BE=9,
∴点F的坐标是(-3,-9).
故答案为(-3,-9).
点评 本题综合考查了圆形的性质和坐标的确定以及勾股定理的运用和矩形的判定及其性质,是综合性较强,难度中等的综合题,解题的关键是根据勾股定理求出⊙P的半径,从而得到F的坐标.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.下列事件中是必然事件的是( )
| A. | 三角形内心到三个顶点的距离相等 | B. | 方程x2-2x+1=0有两个不等实根 | ||
| C. | y=ax2+bx+c是二次函数 | D. | 圆的切线垂直于经过切点的半径 |
10.1米长的彩带,第1次剪去$\frac{1}{3}$,第二次剪去剩下的$\frac{1}{3}$,如此剪下去,剪7次后剩下的彩带长(不计损耗)为( )
| A. | ($\frac{1}{3}$)6米 | B. | ($\frac{1}{3}$)7米 | C. | ($\frac{2}{3}$)6米 | D. | ($\frac{2}{3}$)7米 |
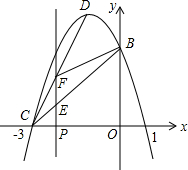 如图,抛物线y=ax2+bx+c与x轴的交点为点A(1,0)和点C(-3,0),与y轴的交点为点B(0,3).
如图,抛物线y=ax2+bx+c与x轴的交点为点A(1,0)和点C(-3,0),与y轴的交点为点B(0,3).