题目内容
13.现用棱长为1cm的若干小立方体,按如图所示的规律在地上搭建若个几何体.图中每个几何体自上而下分别叫第一层,第二层…第n层(n为正整数),其中第一层摆放一个小立方体,第二层摆放4个小立方体,第三层摆放9个小立方体…,依次按此规律继续摆放.(1)求搭建第4个几何体需要的小立方体个数;
(2)为了美观,若将每个几何体的所有露出部分(不包含底面)都喷涂油漆,已知喷涂1cm2需要油漆0.2g.
①求喷涂第4个几何体需要油漆多少g?
②求喷涂第n个几何体需要油漆多少g?(用含n的代数式表示)

分析 (1)观察得到每层向上的面都为正方形,即每层的个数都为平方数,则搭建第4个几何体的小立方体的个数=1+4+9+16;第n个几何体第n层的个数为n2,所以总数为1+22+32+42+…+n2;
(2)①喷漆第四个几何露在外面的表面积为:4×(1+2+3+4)+42=56(cm2),再用表面积×0.2,即可解答.
②第n个几何体的所有露出部分(不含底面)的面积=4×(1+2+3+…+n)+n2,化简后乘以0.2即可.
解答 解:(1)搭建第4个几何体的小立方体的个数=1+4+9+16=30;
(2)①喷漆第四个几何露在外面的表面积为:4×(1+2+3+4)+42=56(cm2),
56×0.2=11.2(g).
②第n个几何体的所有露出部分(不含底面)的面积=4×(1+2+3+…+n)+n2=4×$\frac{n(n+1)}{2}$+n2=3n2+2n,
所以所需要的油漆量=(3n2+2n)×0.2=(0.6n2+0.4n)g.
点评 此题主要考查了图形的变化类:通过特殊图象找到图象变化,归纳总结出规律,再利用规律解决问题.也考查了三视图.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.下列运算中,正确的是( )
| A. | a•a2=a3 | B. | (3a)2=3a2 | C. | 3a6÷a3=3a2 | D. | (ab2)2=a2b2 |
5. 我市某中学举行“中国梦•校园好声音”歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.
我市某中学举行“中国梦•校园好声音”歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.
(1)根据图示填写下表;
(2)计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.
 我市某中学举行“中国梦•校园好声音”歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.
我市某中学举行“中国梦•校园好声音”歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.(1)根据图示填写下表;
(2)计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.
| 平均数(分) | 中位数(分) | 众数(分) | |
| 初中部 | 85 | 85 | 85 |
| 高中部 | 85 | 80 | 100 |
2. 我市某中学七、八年级各选派10名选手参加学校举办的环保知识竞赛,计分采用10分制,选手得分均为整数,成绩达到6分或6分以上为合格,达到9分或10分为优秀,这次竞赛后,七、八年级两支代表队选手成绩分布的条形统计图和成绩统计分析表(不完整)如下所示:
我市某中学七、八年级各选派10名选手参加学校举办的环保知识竞赛,计分采用10分制,选手得分均为整数,成绩达到6分或6分以上为合格,达到9分或10分为优秀,这次竞赛后,七、八年级两支代表队选手成绩分布的条形统计图和成绩统计分析表(不完整)如下所示:
(1)观察条形统计图,可以发现:八年级成绩的标准差<,七年级成绩的标准差(填“>”、“<”或“=”),表格中m=6,n=7.5;
(2)计算七年级的平均分;
(3)有人说七年级的合格率、优秀率均高于八年级,所以七年级队成绩比八年级队好,但也有人说八年级队成绩比七年级队好.请你给出两条支持八年级队成绩好的理由.
 我市某中学七、八年级各选派10名选手参加学校举办的环保知识竞赛,计分采用10分制,选手得分均为整数,成绩达到6分或6分以上为合格,达到9分或10分为优秀,这次竞赛后,七、八年级两支代表队选手成绩分布的条形统计图和成绩统计分析表(不完整)如下所示:
我市某中学七、八年级各选派10名选手参加学校举办的环保知识竞赛,计分采用10分制,选手得分均为整数,成绩达到6分或6分以上为合格,达到9分或10分为优秀,这次竞赛后,七、八年级两支代表队选手成绩分布的条形统计图和成绩统计分析表(不完整)如下所示:| 队别 | 平均分 | 中位数 | 方差 | 合格率 | 优秀率 |
| 七年级 | m | 3.41 | 90% | 20% | |
| 八年级 | 7.1 | n | 80% | 10% |
(2)计算七年级的平均分;
(3)有人说七年级的合格率、优秀率均高于八年级,所以七年级队成绩比八年级队好,但也有人说八年级队成绩比七年级队好.请你给出两条支持八年级队成绩好的理由.
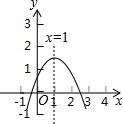 二次函数y=ax2+bx+c(a≠0)图象如图,下列结论:
二次函数y=ax2+bx+c(a≠0)图象如图,下列结论: 如图,在平面直角坐标系中,⊙P与x轴相切于原点O,平行于y轴的直线交⊙P于E,F两点,若点E的坐标是(-3,-1),则点F的坐标是(-3,-9).
如图,在平面直角坐标系中,⊙P与x轴相切于原点O,平行于y轴的直线交⊙P于E,F两点,若点E的坐标是(-3,-1),则点F的坐标是(-3,-9).