题目内容
6.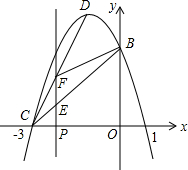 如图,抛物线y=ax2+bx+c与x轴的交点为点A(1,0)和点C(-3,0),与y轴的交点为点B(0,3).
如图,抛物线y=ax2+bx+c与x轴的交点为点A(1,0)和点C(-3,0),与y轴的交点为点B(0,3).(1)求抛物线关系式.(最后结果写成y=ax2+bx+c的形式)
(2)若顶点为点D,连接CD、CB,在x轴上取一动点P(m,0),m的取值范围是-3<m<-1,过点P作x轴的垂线,分别交CD、CB于点F、E,连接BF.
①判断EF与EP的长度关系,并说明理由.
②在点P运动过程中,△BEF可以为等腰三角形吗?求m的值;若不能,说明理由.
分析 (1)利用待定系数法即可求得函数的解析式;
(2)①首先利用待定系数法求得直线BC和CD的解析式,则EF和EP的长可以利用m表示出来,从而证得;
②利用m表示出△BEF的三边长,然后分成三种情况讨论,解方程求解即可.
解答 解:(1)根据题意得:$\left\{\begin{array}{l}{a+b+c=0}\\{9a-3b+c=0}\\{c=3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-1}\\{b=-2}\\{c=3}\end{array}\right.$,
则抛物线的解析式是y=-x2-2x+3;
(2)①EF=EP.
理由是:y=-x2-2x+3=-(x+1)2+4,
则D的坐标是(-1,4).
设直线BC的解析式是y=kx+b,则$\left\{\begin{array}{l}{-3k+b=0}\\{b=3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=1}\\{b=3}\end{array}\right.$,
则直线BC的解析式是y=x+3.
同理,直线CD的解析式是y=2x+6.
∵动点P(m,0)在x轴上,-3<m<-1,且PF⊥x轴.
∴点E(m,m+3),点F(m,2m+6),即PE=m+3,PF=2m+6.EF=PF-PE=(2m+6)-(m+3)=m+3.
∴EF=EP;
②点E(m,m+3),点F(m,2m+6),点B(0,3),-3<m<-1.
若△BEF为等腰三角形时,分成三种情况讨论.
1)当BF=EF时,则$\sqrt{{m}^{2}+(2m+3)^{2}}$=m+3,
解得:m=-$\frac{3}{2}$或0(舍去);
2)当BF=BE时,$\sqrt{{m}^{2}+(2m+3)^{2}}$=$\sqrt{{m}^{2}+{m}^{2}}$,
解得:m=-1(舍去)或-3(舍去);
3)当EF=BE时,则$\sqrt{{m}^{2}+{m}^{2}}$=m+3,解得m=3+3$\sqrt{2}$(舍去)或3-3$\sqrt{2}$.
总上所述,符合要求的m的值有2个,分别是-$\frac{3}{2}$和3-3$\sqrt{2}$.
点评 本题考查了待定系数法求函数解析式,以及等腰三角形的讨论,正确利用m表示出△BEF的边长是关键.

| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | 3 | D. | -3 |
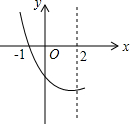 如图,是抛物线y=ax2+bx+c(a≠0)的一部分,已知抛物线的对称轴为x=2,与x轴的一个交点是(-1,0),则方程ax2+bx+c=0(a≠0)的两根是x1=-1,x2=5.
如图,是抛物线y=ax2+bx+c(a≠0)的一部分,已知抛物线的对称轴为x=2,与x轴的一个交点是(-1,0),则方程ax2+bx+c=0(a≠0)的两根是x1=-1,x2=5.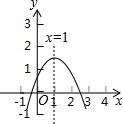 二次函数y=ax2+bx+c(a≠0)图象如图,下列结论:
二次函数y=ax2+bx+c(a≠0)图象如图,下列结论: 如图,在Rt△ACB中,∠C=90°,AC=30cm,BC=25cm,动点P从点C出发,沿CA方向运动,速度是2cm/s,动点Q从点B出发,沿BC方向运动,速度是1cm/s.
如图,在Rt△ACB中,∠C=90°,AC=30cm,BC=25cm,动点P从点C出发,沿CA方向运动,速度是2cm/s,动点Q从点B出发,沿BC方向运动,速度是1cm/s. 如图,在平面直角坐标系中,⊙P与x轴相切于原点O,平行于y轴的直线交⊙P于E,F两点,若点E的坐标是(-3,-1),则点F的坐标是(-3,-9).
如图,在平面直角坐标系中,⊙P与x轴相切于原点O,平行于y轴的直线交⊙P于E,F两点,若点E的坐标是(-3,-1),则点F的坐标是(-3,-9). 如图,将一张正方形铁片的4个角剪去4个大小一样的小正方形,然后折起来就可以制成一个无盖的长方体容器,设这个正方形铁片的边长为a,做成的无盖长方体容器高为h.
如图,将一张正方形铁片的4个角剪去4个大小一样的小正方形,然后折起来就可以制成一个无盖的长方体容器,设这个正方形铁片的边长为a,做成的无盖长方体容器高为h.