题目内容
15.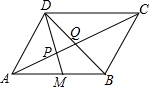 如图,已知在平行四边形ABCD中,M为AB的中点,DM,DB分别交AC于P,Q两点,则AP:PQ:QC=2:1:3.
如图,已知在平行四边形ABCD中,M为AB的中点,DM,DB分别交AC于P,Q两点,则AP:PQ:QC=2:1:3.
分析 由在平行四边形ABCD中,M为AB的中点,可证得△APM∽△CPD,根据相似三角形的对应边成比例,可求得AP:AC的值,继而求得PQ:AC与QC:AC的值,则可求得答案.
解答 解:∵四边形ABCD是平行四边形,
∴AQ=CQ,AB∥CD,AB=CD,
∴△APM∽△CPD,
∴AP:PC=AM:CD,
∵M为AB的中点,
∴AM:CD=AM:AB=1:2,
∴AP:PC=1:2,
∴AP:AC=1:3,
∵AQ:AC=QC:AC=1:2,
∴PQ:AC=1:6,
∴AP:PQ:QC=$\frac{1}{3}$AC:$\frac{1}{6}$AC:$\frac{1}{2}$AC=2:1:3.
故答案为:2:1:3.
点评 此题考查了相似三角形的判定与性质以及平行四边形的性质.注意分别求得各线段与AC的关系是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.已知k、m为实数,在平面直角坐标系中,对于任意的实数k,点P(k2+1,-k2+2k+m)都在第四象限,则m的取值范围是( )
| A. | m>-1 | B. | m=-1 | C. | m>1 | D. | m<-1 |
20.计算(-2)÷3×$\frac{1}{3}$的结果为( )
| A. | 2 | B. | -2 | C. | -$\frac{2}{9}$ | D. | $\frac{2}{9}$ |