题目内容
5．在直线上依次取点A、B、C、D，且使得AB：BC：CD=3：4：5，若AB的中点M与CD的中点N的距离为10cm，求线段AB的长度．分析 根据AB：BC：CD=3：4：5，可得AB=3x，BC=4x，CD=5x，根据线段中点的性质，可得MB，CN的长，根据线段和差，可得x的值．
解答 解：如图：
，
由AB：BC：CD=3：4：5，可设AB=3x，BC=4x，CD=5x．
由AB：BC：CD=3：4：5，得
MB=$\frac{1}{2}$AB=$\frac{3x}{2}$，CN=$\frac{1}{2}$CD=2x，
由线段的和差，得
MN=MB+BC+CN=$\frac{3x}{2}$+4x+$\frac{5x}{2}$=10，
解得x=$\frac{5}{4}$，
AB=3x=3×$\frac{5}{4}$=$\frac{15}{4}$．
点评 本题考查了两点间的距离，利用线段的和差得出关于x的方程是解题关键，又利用了线段中点的性质．
练习册系列答案
一本好题口算题卡系列答案
相关题目
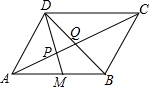如图，已知在平行四边形ABCD中，M为AB的中点，DM，DB分别交AC于P，Q两点，则AP：PQ：QC=2：1：3．