题目内容
11.公式:(x+y+z)2=x2+y2+z2+2(xy+yz+xz).若现有三实数a、b、c,满足a+b+c=0,abc=6,则$\frac{1}{a}$$+\frac{1}{b}$$+\frac{1}{c}$为( )| A. | 正数 | B. | 负数 | C. | 零 | D. | 非负数 |
分析 首先将原式通分再进行变形,进而利用已知公式分析得出答案.
解答 解:$\frac{1}{a}$$+\frac{1}{b}$$+\frac{1}{c}$=$\frac{bc}{abc}$+$\frac{ac}{abc}$+$\frac{ab}{abc}$
=$\frac{bc+ac+ab}{abc}$
∵(x+y+z)2=x2+y2+z2+2(xy+yz+xz),a+b+c=0,
∴(a+b+c)2=a2+b2+c2+2(ab+bc+ac)=0,
∴a2+b2+c2=-2(ab+bc+ac),
∵abc=6,∴a,b,c都不为0,
∴ab+bc+ac<0,
∴$\frac{bc+ac+ab}{abc}$=$\frac{ba+bc+ac}{6}$<0.
故选:B.
点评 此题主要考查了完全平方公式的应用,正确将原式变形是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.当棱长为20cm正方体的某个面平行于投影面时,这个面的正投影的面积为( )
| A. | 20cm2 | B. | 300cm2 | C. | 400cm2 | D. | 600cm2 |
20.下列四个几何体中左视图与俯视图相同的几何体是( )


| A. | ①② | B. | ①③ | C. | ②③ | D. | ③④ |
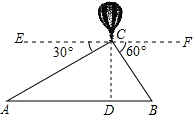 如图所示,从热气球C上测定建筑物A、B底部的俯角分别为30°和60°,已知AB间的距离为180米,CD垂直于AB于点D.问:此时热气球的高度为多少?
如图所示,从热气球C上测定建筑物A、B底部的俯角分别为30°和60°,已知AB间的距离为180米,CD垂直于AB于点D.问:此时热气球的高度为多少? 如图,AB是⊙O的直径,∠D=20°.求∠BAC的度数.
如图,AB是⊙O的直径,∠D=20°.求∠BAC的度数.