题目内容
已知正比例函数y=k1x(k1≠0)与反比例函数y=
(k2≠0)的图象有一个交点的坐标为(-2,-1 ),则它们的另一个交点的坐标是( )
| k2 |
| x |
| A、(2,1) |
| B、(-2,-1) |
| C、(-2,1) |
| D、(2,-1) |
考点:反比例函数与一次函数的交点问题
专题:
分析:把已知点的坐标代入两函数解析式可求出函数解析式,再联立两函数解析式可求得另一个交点的坐标.
解答:解:
∵两函数图象的一个交点坐标为(-2,-1),
∴-1=-2k1,-1=
,
解得k1=
,k2=2,
∴正比例函数为y=
x,反比例函数为y=
,
联立两函数解析式可得
,解得
或
,
∴两函数图象的另一交点坐标为(2,1),
故选A.
∵两函数图象的一个交点坐标为(-2,-1),
∴-1=-2k1,-1=
| k2 |
| -2 |
解得k1=
| 1 |
| 2 |
∴正比例函数为y=
| 1 |
| 2 |
| 2 |
| x |
联立两函数解析式可得
|
|
|
∴两函数图象的另一交点坐标为(2,1),
故选A.
点评:本题主要考查函数图象的交点,利用待定系数法求得两函数解析式是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①c<0,②b>0,③4a+2b+c>0,④(a+c)2<b2,⑤b+2a=0;⑥△<0,其中正确的是
二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①c<0,②b>0,③4a+2b+c>0,④(a+c)2<b2,⑤b+2a=0;⑥△<0,其中正确的是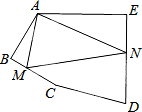 如图,在五边形ABCDE中,∠BAE=125°,∠B=∠E=90°,AB=BC,AE=DE,在BC、DE上分别找一点M、N,使得△AMN周长最小时,∠AMN+∠ANM的度数为
如图,在五边形ABCDE中,∠BAE=125°,∠B=∠E=90°,AB=BC,AE=DE,在BC、DE上分别找一点M、N,使得△AMN周长最小时,∠AMN+∠ANM的度数为 如图,图中有
如图,图中有