题目内容
已知△ABC是圆O的内接三角形,P是△ABC的内心,AP交BC于D,交圆O于E,延长AE至F,PE=EF,求证:PC⊥FC.
考点:三角形的内切圆与内心
专题:证明题
分析:根据三角形内心的定义得到∠5=∠6,∠2=∠3,利用三角形外角性质得∠1=∠5+∠2=∠5+∠3,再根据圆周角定理得到∠4=∠6,所以∠4=∠5,则∠1=∠3+∠4,即∠1=∠PCE,得到EC=EP,于是有PE=EF=EC,根据等腰三角形的性质得∠7=∠F,利用三角形内角和定理可计算出∠3+∠4+∠7=90°,然后根据垂直的定义即可得到结论.
解答: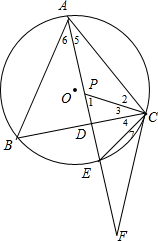 证明:∵P是△ABC的内心,
证明:∵P是△ABC的内心,
∴PA平分∠BAC,PC平分∠ACB,
∴∠5=∠6,∠2=∠3,
∴∠1=∠5+∠2=∠5+∠3,
∵∠4=∠6,
∴∠4=∠5,
∴∠1=∠3+∠4,即∠1=∠PCE,
∴EC=EP,
∵PE=EF,
∴PE=EF=EC,
∴∠7=∠F,
∴∠3+∠4+∠7=
×180°=90°,
∴PC⊥FC.
 证明:∵P是△ABC的内心,
证明:∵P是△ABC的内心,∴PA平分∠BAC,PC平分∠ACB,
∴∠5=∠6,∠2=∠3,
∴∠1=∠5+∠2=∠5+∠3,
∵∠4=∠6,
∴∠4=∠5,
∴∠1=∠3+∠4,即∠1=∠PCE,
∴EC=EP,
∵PE=EF,
∴PE=EF=EC,
∴∠7=∠F,
∴∠3+∠4+∠7=
| 1 |
| 2 |
∴PC⊥FC.
点评:本题考查了三角形的内切圆与内心:与三角形各边都相切的圆叫三角形的内切圆,三角形的内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形.三角形的内心就是三角形三个内角角平分线的交点.也考查了圆周角定理.

练习册系列答案
相关题目
已知正比例函数y=k1x(k1≠0)与反比例函数y=
(k2≠0)的图象有一个交点的坐标为(-2,-1 ),则它们的另一个交点的坐标是( )
| k2 |
| x |
| A、(2,1) |
| B、(-2,-1) |
| C、(-2,1) |
| D、(2,-1) |
在Rt△ABC中,∠C=90°,sinA=
,下列错误的是( )
| 5 |
| 13 |
A、cosA=
| ||
B、cosB=
| ||
C、sinB=
| ||
D、tanB=
|
 如图所示,在Rt△ABC中,∠BAC=90°,AB=AC=3,E,D分别是BC、AC上的点,∠AED=45°,BE=1,求CD的长.
如图所示,在Rt△ABC中,∠BAC=90°,AB=AC=3,E,D分别是BC、AC上的点,∠AED=45°,BE=1,求CD的长. 如图,已知⊙O的半径为10,点C、D是直径AB同侧圆周上的两点,
如图,已知⊙O的半径为10,点C、D是直径AB同侧圆周上的两点,
 如图,△ABC的高AD、BE交于点F,求证:
如图,△ABC的高AD、BE交于点F,求证: