题目内容
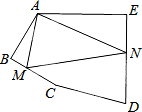如图，在五边形ABCDE中，∠BAE=125°，∠B=∠E=90°，AB=BC，AE=DE，在BC、DE上分别找一点M、N，使得△AMN周长最小时，∠AMN+∠ANM的度数为考点：轴对称-最短路线问题
专题：
分析：取点A关于BC的对称点P，关于DE的对称点Q，连接PQ与BC相交于点M，与DE相交于点N，根据轴对称的性质可得AM=PM，AN=QN，然后求出△AMN周长=PQ，根据轴对称确定最短路线问题，PQ的长度即为△AMN的周长最小值，根据三角形的内角和等于180°求出∠P+∠Q，再根据三角形的一个外角等于与它不相邻的两个内角的和求出∠AMN=2∠P，∠ANM=2∠Q，然后求解即可．
解答：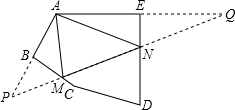
解：如图，取点A关于BC的对称点P，关于DE的对称点Q，连接PQ与BC相交于点M，与DE相交于点N，
则AM=PM，AN=QN，
所以，∠P=∠PAM，∠Q=∠QAN，
所以，△AMN周长=AM+MN+AN=PM+MN+QN=PQ，
由轴对称确定最短路线，PQ的长度即为△AMN的周长最小值，
∵∠BAE=125°，
∴∠P+∠Q=180°-125°=55°，
∵∠AMN=∠P+∠PAM=2∠P，∠ANM=∠Q+∠QAN=2∠Q，
∴∠AMN+∠ANM=2（∠P+∠Q）=2×55°=110°．
故答案为：110°．
解：如图，取点A关于BC的对称点P，关于DE的对称点Q，连接PQ与BC相交于点M，与DE相交于点N，则AM=PM，AN=QN，
所以，∠P=∠PAM，∠Q=∠QAN，
所以，△AMN周长=AM+MN+AN=PM+MN+QN=PQ，
由轴对称确定最短路线，PQ的长度即为△AMN的周长最小值，
∵∠BAE=125°，
∴∠P+∠Q=180°-125°=55°，
∵∠AMN=∠P+∠PAM=2∠P，∠ANM=∠Q+∠QAN=2∠Q，
∴∠AMN+∠ANM=2（∠P+∠Q）=2×55°=110°．
故答案为：110°．
点评：本题考查了利用轴对称确定最短路线问题，等边对等角的性质，三角形的内角和定理，确定出点M、N的位置是解题的关键，作出图形更形象直观．
练习册系列答案
相关题目
下列说法正确的是（ ）
| A、过A，B两点的直线长是A，B两点间的距离 |
| B、线段AB是A、B两点间的距离 |
| C、射线AB是A，B两点间的距离 |
| D、连接A，B两点的所有线中，线段AB的长度就是A，B两点间的距离 |
已知正比例函数y=k1x（k1≠0）与反比例函数y=
（k2≠0）的图象有一个交点的坐标为（-2，-1 ），则它们的另一个交点的坐标是（ ）
| k2 |
| x |
| A、（2，1） |
| B、（-2，-1） |
| C、（-2，1） |
| D、（2，-1） |
如图，已知⊙O的半径为10，点C、D是直径AB同侧圆周上的两点，
如图，△ABC的高AD、BE交于点F，求证：-3的相反数是（ ）
| A、3 | ||
B、
| ||
| C、-3 | ||
D、-
|