题目内容
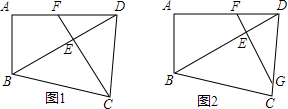
5．
如图是四张全等的矩形纸片拼成的图形，利用图中阴影部分面积的不同表示方法，可以写出关于a、b的恒等式，下列各式正确的为（ ）| A． | （a+b）2=（a-b）2+2ab | B． | （a-b）2=（a+b）2-2ab | C． | （a-b）2=a2-2ab+b2 | D． | （a+b）（a-b）=a2-b2 |
分析 从图中可以得出，大正方形的边长为a+b，大正方形的面积就为（a+b）2，4个矩形完全相同，且长为a，宽为b，则4个矩形的面积为4ab，中间的正方形的边长为a-b，面积等于（a-b）2，大正方形面积减去4个矩形的面积就等于中间阴影部分的面积．
解答 解：∵四周部分都是全等的矩形，且长为a，宽为b，
∴四个矩形的面积为4ab，
∵大正方形的边长为a+b，
∴大正方形面积为（a+b）2，
∴中间小正方形的面积为（a+b）2-4ab=a2-2ab+b2，
而中间小正方形的面积也可表示为：（a-b）2，
∴（a-b）2=a2-2ab+b2．
故选：C．
点评 本题考查了完全平方公式几何意义，利用正方形面积和矩形的面积的计算方法解决问题．
练习册系列答案
赢在课堂名师课时计划系列答案
天天向上课时同步训练系列答案
相关题目
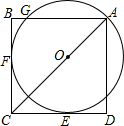如图．圆心O在边长为2$\sqrt{2}$的正方形ABCD的对角线AC上，⊙O过点A，且BC，CD都相切，求$\widehat{AG}$的长．