题目内容
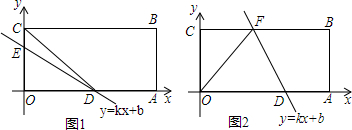
13．将正方体骰子（相对面上的点数分别为1和6、2和5、3和4）放置于水平桌面上，如图1．在图2中，将骰子向右翻滚90度，然后在桌面上按逆时针方向旋转90度，则完成一次变换．若骰子的初始位置为图1所示的状态，那么按上述规则连续完成32次变换后，骰子朝上一面的点数是（ ）
| A． | 6 | B． | 5 | C． | 3 | D． | 2 |
分析 先向右翻滚，然后再逆时针旋转叫做一次变换，那么连续3次变换是一个循环．本题先要找出3次变换是一个循环，然后再求32被3整除后余数是2，从而确定第1次变换的第2步变换．
解答 解：根据题意可知连续3次变换是一循环．
因为32÷3=10…2，
所以是第2次变换后的图形．
故选：A．
点评 本题考查了正方体相对两个面上的文字，解决本题的关键是找到规律．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
4．已知扇形的圆心角为120°，半径为6cm的圆，则扇形的弧长为（ ）
| A． | 3cm | B． | 3πcm | C． | 4cm | D． | 4πcm |
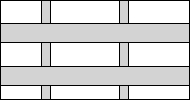如图，要设计一副宽20cm，长30cm的图象，其中两幅两竖的彩条，横竖彩条的宽度比为2：1，如果要使彩条所占面积是图案面积是$\frac{19}{75}$，那么竖彩条宽度为多少？
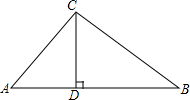如图，在Rt△ABC中，∠ACB=90°，CD⊥AB，垂足为D，CD=8，AC=10．
已知在正方形ABCD中，CE=3DE，AF⊥BE，求sin∠BAF的值．
5．
如图是四张全等的矩形纸片拼成的图形，利用图中阴影部分面积的不同表示方法，可以写出关于a、b的恒等式，下列各式正确的为（ ）
如图是四张全等的矩形纸片拼成的图形，利用图中阴影部分面积的不同表示方法，可以写出关于a、b的恒等式，下列各式正确的为（ ）| A． | （a+b）2=（a-b）2+2ab | B． | （a-b）2=（a+b）2-2ab | C． | （a-b）2=a2-2ab+b2 | D． | （a+b）（a-b）=a2-b2 |
