题目内容
17.如图,四边形ABCD中,∠A=∠BCD=90°.(1)过C作对角线BD的垂线交BD、AD于点E、F,求证:CD2=DF•DA;
(2)如图2:若过BD上另一点E作BD的垂线交DA、DC于点F、G,有什么结论?并证明.
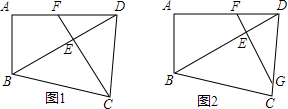
分析 (1)根据如果两个三角形的两个对应角相等,那么这两个三角形相似,可以证得△DCE∽△DBC,△DEF∽△DAB;根据相似三角形的对应边成比例,即可证得.
(2)利用上题的方法,可以得到比例线段,将其变形,可得到等积式.
解答 证明:(1)∵∠DEF=∠DAB=90°,∠BDA=∠FDE,
∴△DEF∽△DAB,
∴DE:DA=DF:DB,
∴DE•DB=DA•DF,
∵∠DCB=∠DEC=90°,∠BDC=∠CDE,
∴△DEC∽△DCB,
∴$\frac{CD}{DE}=\frac{DB}{CD}$,
∴DC2=DE•DB,
又∵DE•DB=DA•DF,
∴CD2=DF•DA.
(2)∵∠DEF=∠DAB=90°,∠ADB=∠FDE,
∴△DEF∽△DAB,
∴DE:DA=DF:DB,
∴DE•DB=DA•DF,
同理△DBC∽△GDE.
∴DB:GD=DC:DE.
∴DE•BD=CD•DG.
∴AB•DF=DC•DG.
点评 本题考查了相似三角形的判定和性质,熟记掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
5. 如图是四张全等的矩形纸片拼成的图形,利用图中阴影部分面积的不同表示方法,可以写出关于a、b的恒等式,下列各式正确的为( )
如图是四张全等的矩形纸片拼成的图形,利用图中阴影部分面积的不同表示方法,可以写出关于a、b的恒等式,下列各式正确的为( )
 如图是四张全等的矩形纸片拼成的图形,利用图中阴影部分面积的不同表示方法,可以写出关于a、b的恒等式,下列各式正确的为( )
如图是四张全等的矩形纸片拼成的图形,利用图中阴影部分面积的不同表示方法,可以写出关于a、b的恒等式,下列各式正确的为( )| A. | (a+b)2=(a-b)2+2ab | B. | (a-b)2=(a+b)2-2ab | C. | (a-b)2=a2-2ab+b2 | D. | (a+b)(a-b)=a2-b2 |
9.下列计算正确的是( )
| A. | ($\frac{2{a}^{-3}b}{-{c}^{3}}$)2=$\frac{4{a}^{9}b}{{c}^{5}}$ | B. | ($\frac{2x-y}{-5{a}^{2}}$)2=$\frac{4{x}^{2}-{y}^{2}}{25{a}^{4}}$ | ||
| C. | (3xny-n)-m=$\frac{{y}^{mn}}{{3}^{m}x^{mn}}$ | D. | (-$\frac{{b}^{2}}{a}$)2n=-$\frac{{b}^{2+2n}}{{a}^{n}}$ |
19.下列各式去括号正确的是( )
| A. | -(a+b)=a-b | B. | 2(x-2)=2x-2 | C. | -3(2x-1)=-6x-3 | D. | 2-(-x+3)×2=2+2x-6 |
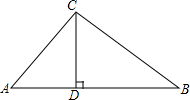 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,CD=8,AC=10.
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,CD=8,AC=10.