题目内容
20.在△ABC中∠A=30°,AC=$\sqrt{3}$,BC=1,则∠B=60°.分析 根据在△ABC中∠A=30°,AC=$\sqrt{3}$,BC=1,可以求得该三角形为直角三角形,从而可以求得∠B的度数.
解答 解:∵在△ABC中∠A=30°,AC=$\sqrt{3}$,BC=1,
∴$\frac{BC}{AC}=\frac{1}{\sqrt{3}}=\frac{\sqrt{3}}{3}$,tan30°=$\frac{\sqrt{3}}{3}$.
∴△ABC是直角三角形,∠C=90°.
∴∠B=90°-∠A=90°-30°=60°.
故答案为:60°.
点评 本题考查解直角三角形,解题的关键是根据边的比值可以判断角的度数.

练习册系列答案
相关题目
5. 如图是四张全等的矩形纸片拼成的图形,利用图中阴影部分面积的不同表示方法,可以写出关于a、b的恒等式,下列各式正确的为( )
如图是四张全等的矩形纸片拼成的图形,利用图中阴影部分面积的不同表示方法,可以写出关于a、b的恒等式,下列各式正确的为( )
 如图是四张全等的矩形纸片拼成的图形,利用图中阴影部分面积的不同表示方法,可以写出关于a、b的恒等式,下列各式正确的为( )
如图是四张全等的矩形纸片拼成的图形,利用图中阴影部分面积的不同表示方法,可以写出关于a、b的恒等式,下列各式正确的为( )| A. | (a+b)2=(a-b)2+2ab | B. | (a-b)2=(a+b)2-2ab | C. | (a-b)2=a2-2ab+b2 | D. | (a+b)(a-b)=a2-b2 |
9.下列计算正确的是( )
| A. | ($\frac{2{a}^{-3}b}{-{c}^{3}}$)2=$\frac{4{a}^{9}b}{{c}^{5}}$ | B. | ($\frac{2x-y}{-5{a}^{2}}$)2=$\frac{4{x}^{2}-{y}^{2}}{25{a}^{4}}$ | ||
| C. | (3xny-n)-m=$\frac{{y}^{mn}}{{3}^{m}x^{mn}}$ | D. | (-$\frac{{b}^{2}}{a}$)2n=-$\frac{{b}^{2+2n}}{{a}^{n}}$ |
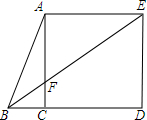 如图,在Rt△ABC中,∠ACB=90°,∠ABC=60°,以AC为边向三角形外作正方形ACDE,连接BE交AC于F.若BF=$\sqrt{3}$cm,则EF=3.
如图,在Rt△ABC中,∠ACB=90°,∠ABC=60°,以AC为边向三角形外作正方形ACDE,连接BE交AC于F.若BF=$\sqrt{3}$cm,则EF=3.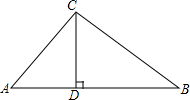 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,CD=8,AC=10.
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,CD=8,AC=10.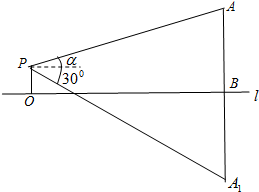 在湖心有一座塔,小明想知道这座塔的高度,于是他在岸边架起了测角仪.他测量得数据如下(如图示):测角仪位置(P)距水平面(l)的距离为1.5米(即OP),测得塔顶A的仰角为α(其中tanα=$\frac{1}{3}$),测得塔顶在水中倒影A1(即AB=A1B)的俯角为300.那么这座塔的高度AB=3+$\frac{3\sqrt{3}}{2}$.(结果保留根号)
在湖心有一座塔,小明想知道这座塔的高度,于是他在岸边架起了测角仪.他测量得数据如下(如图示):测角仪位置(P)距水平面(l)的距离为1.5米(即OP),测得塔顶A的仰角为α(其中tanα=$\frac{1}{3}$),测得塔顶在水中倒影A1(即AB=A1B)的俯角为300.那么这座塔的高度AB=3+$\frac{3\sqrt{3}}{2}$.(结果保留根号)