题目内容
9.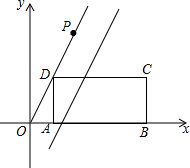 如图,在平面直角坐标系中,矩形ABCD的边AB在x轴的正半轴上,点A在点B的左侧,直线y=kx经过点D(1,2)和点P,已知OP=2$\sqrt{5}$,将直线y=kx沿y轴向下平移得到y=kx+b,若点P落在矩形ABCD的内部,那么b的取值范围是( )
如图,在平面直角坐标系中,矩形ABCD的边AB在x轴的正半轴上,点A在点B的左侧,直线y=kx经过点D(1,2)和点P,已知OP=2$\sqrt{5}$,将直线y=kx沿y轴向下平移得到y=kx+b,若点P落在矩形ABCD的内部,那么b的取值范围是( )| A. | 0<b<2 | B. | -2<b<0 | C. | -4<b<-2 | D. | -4<b<2 |
分析 作DE⊥CD于E交AB于F,先求出直线y=kx以及点P坐标,再确定点E、F坐标,代入y=2x+b中即可解决问题.
解答 解:如图作DE⊥CD于E交AB于F,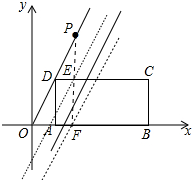
∵点D(1,2)在直线y=kx上,
∴k=2,
∴直线为y=2x,设点P坐标(a,2a),
∵OP=2$\sqrt{5}$,
∴a2+4a2=20,
∴a2=4,
∵a>0,
∴a=2.
∴点P坐标(2,4),点E(2,2),点F(2,0),
把点E(2,2),点F(2,0),分别代入y=2x+b中,得到b=-2或-4,
∴点P落在矩形ABCD的内部,
∴-4<b<-2.
故选C.
点评 本题考查一次函数有关知识,掌握两条直线平行k相同,寻找特殊点是解决问题的关键,理解点P在平移过程中与y轴的距离保持不变,属于中考常考题型.

练习册系列答案
相关题目
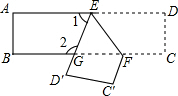 把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D、C分别在D′、C′的位置上.如图所示,若∠EFG=60°,求∠1与∠2的度数.
把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D、C分别在D′、C′的位置上.如图所示,若∠EFG=60°,求∠1与∠2的度数.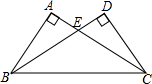 如图,∠BAC=90°,∠EDC=90°,∠DCE=30°,ED=2,AB=3,求S△CEB的值.
如图,∠BAC=90°,∠EDC=90°,∠DCE=30°,ED=2,AB=3,求S△CEB的值. 如图,已知AB∥DC,AD∥BC,且∠1=∠2,求证:∠3=∠4.
如图,已知AB∥DC,AD∥BC,且∠1=∠2,求证:∠3=∠4.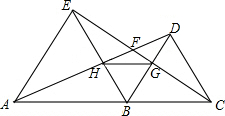 已知点A、B、C三点共线,分别以线段AB、BC为边作等边△ABE,△DBC,连接AD、EC.
已知点A、B、C三点共线,分别以线段AB、BC为边作等边△ABE,△DBC,连接AD、EC. 如图,在?ABCD中.点O是对角线AC、BD的交点,AC垂直于BC.且AB=10cm,AD=8cm,求OB的长.
如图,在?ABCD中.点O是对角线AC、BD的交点,AC垂直于BC.且AB=10cm,AD=8cm,求OB的长.