题目内容
17．已知$\left\{\begin{array}{l}{x=4}\\{y=2}\end{array}\right.$是方程组$\left\{\begin{array}{l}{2x+（m-1）y=4}\\{nx+y=2}\end{array}\right.$的解，求（m+n）2014的值．分析 把x与y的值代入方程组求出m与n的值，代入原式计算即可得到结果．
解答 解：把$\left\{\begin{array}{l}{x=4}\\{y=2}\end{array}\right.$代入方程组得：$\left\{\begin{array}{l}{8+2m-2=4}\\{4n+2=2}\end{array}\right.$，
解得：m=-1，n=0，
则原式=1．
点评 此题考查了二元一次方程组的解，方程组的解即为能使方程组左右两边相等的未知数的值．
练习册系列答案
名校课堂系列答案
相关题目
9．
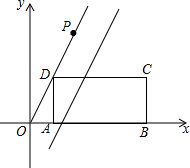如图，在平面直角坐标系中，矩形ABCD的边AB在x轴的正半轴上，点A在点B的左侧，直线y=kx经过点D（1，2）和点P，已知OP=2$\sqrt{5}$，将直线y=kx沿y轴向下平移得到y=kx+b，若点P落在矩形ABCD的内部，那么b的取值范围是（ ）
如图，在平面直角坐标系中，矩形ABCD的边AB在x轴的正半轴上，点A在点B的左侧，直线y=kx经过点D（1，2）和点P，已知OP=2$\sqrt{5}$，将直线y=kx沿y轴向下平移得到y=kx+b，若点P落在矩形ABCD的内部，那么b的取值范围是（ ）| A． | 0＜b＜2 | B． | -2＜b＜0 | C． | -4＜b＜-2 | D． | -4＜b＜2 |
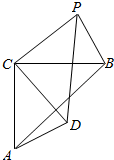如图，等腰直角△ABC，AC=BC=$\sqrt{5}$，等腰直角△CDP中，CD=CP，且PB=$\sqrt{2}$，将△CDP绕点C旋转．
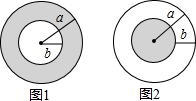如图1，在一个半径为a的大圆内，挖去一个半径为b（0＜b＜a）的小圆，剩下部分（阴影部分）的面积为S1；如图2，在一个半径为a的大圆上剪去一个圆环（内径为b），剩下部分（阴影部分）的面积为S2，则S1与S2的大小关系是（ ）