题目内容
1．
如图，在?ABCD中．点O是对角线AC、BD的交点，AC垂直于BC．且AB=10cm，AD=8cm，求OB的长．
分析 根据平行四边形的性质得到BC=AD=8cm，根据勾股定理即可得到结论．
解答 解：在?ABCD中
∵BC=AD=8cm，
∵AC垂直于BC，
∴∠ACB=90°，
∴AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=6cm，
∵OC=$\frac{1}{2}$AC=3cm，
∴OB=$\sqrt{B{C}^{2}+O{C}^{2}}$=$\sqrt{73}$，
点评 本题考查了平行四边形的性质、勾股定理；熟练掌握平行四边形的性质，并能进行推理计算是解决问题的关键．
练习册系列答案
相关题目
11．点P（m+6，m-3）在y轴上，则点P的坐标是（ ）
| A． | （-3，0） | B． | （0，3） | C． | （0，-9） | D． | （9，0） |
12．在直角坐标系中，点M（$\sqrt{3}$，-2）在（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
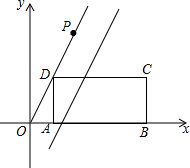如图，在平面直角坐标系中，矩形ABCD的边AB在x轴的正半轴上，点A在点B的左侧，直线y=kx经过点D（1，2）和点P，已知OP=2$\sqrt{5}$，将直线y=kx沿y轴向下平移得到y=kx+b，若点P落在矩形ABCD的内部，那么b的取值范围是（ ）