题目内容
3.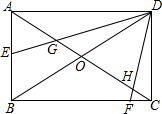 已知:如图,在矩形ABCD中,∠EDF两边分别与边AB、BC交于E、F,与对角线交于G、H,且∠EDF=∠BDC,∠BDC=60°,AE=2,DH=$\sqrt{13}$时,DG=$\frac{4\sqrt{13}}{3}$.
已知:如图,在矩形ABCD中,∠EDF两边分别与边AB、BC交于E、F,与对角线交于G、H,且∠EDF=∠BDC,∠BDC=60°,AE=2,DH=$\sqrt{13}$时,DG=$\frac{4\sqrt{13}}{3}$.
分析 先证明△DEB∽△DHC,得$\frac{DE}{DH}=\frac{DB}{DC}=2$,由此求出DE,利用勾股定理求出AD,CD,根据AE∥CD,得$\frac{AE}{CD}=\frac{EG}{GD}$=$\frac{1}{2}$,即可解决问题.
解答  解:∵四边形ABCD是矩形,
解:∵四边形ABCD是矩形,
∴∠BAD=BCD=90°,AB∥CD,OA=OC=OD=OB,
∴∠ABD=∠BDC=60°,∠DBC=90°-∠BDC=30°,
∴BD=2CD,△ODC是等边三角形,
∴∠DCO=60°,
∵∠EDF=∠BDC=60°,
∴∠EDB=∠DHC,∵∠DEB=∠DCH,
∴△DEB∽△DHC,
∴$\frac{DE}{DH}=\frac{DB}{DC}=2$,
∵DH=$\sqrt{13}$,
∴DE=2$\sqrt{13}$,
在RT△ADE中,∵$AE=2,ED=2\sqrt{13}$,
∴AD=$\sqrt{D{E}^{2}-A{E}^{2}}$=4$\sqrt{3}$,
在RT△ADC中,∵∠DAC=30°,AD=4$\sqrt{3}$,
∵CD=4,
∵AE∥CD,
∴$\frac{AE}{CD}=\frac{EG}{GD}$=$\frac{1}{2}$,
∴DG=$\frac{2}{3}$DE=$\frac{4\sqrt{13}}{3}$.
故答案为$\frac{4\sqrt{13}}{3}$.
点评 本题考查相似三角形的判定和性质、矩形的性质、勾股定理等知识,利用相似三角形的性质是解题的关键,难点是正确寻找相似三角形.

练习册系列答案
相关题目
13.点P为直线l外一点,点A、B在直线l上,若PA=3,PB=5,则点P到直线l的距离为( )
| A. | 3 | B. | 小于3 | C. | 不大于3 | D. | 4 |
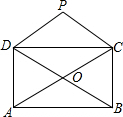 如图,矩形ABCD的对角线相交于点O,PD∥AC,PC∥BD.
如图,矩形ABCD的对角线相交于点O,PD∥AC,PC∥BD.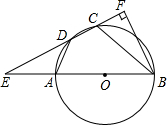 已知四边形ABCD内接于圆O,AB是直径,AD=DC,分别延长BA,CD交于点E,BF垂直EC,交EC的延长线于F.若EA=AO,BC=6,则圆O的半径4,CF的长$\frac{3\sqrt{2}}{2}$.
已知四边形ABCD内接于圆O,AB是直径,AD=DC,分别延长BA,CD交于点E,BF垂直EC,交EC的延长线于F.若EA=AO,BC=6,则圆O的半径4,CF的长$\frac{3\sqrt{2}}{2}$.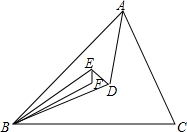 如图,△ABC内一点D,AD、BD、CD分别平分∠A、∠B、∠C,又E是△ABD内一点,AE、BE、CE分别平分△ABD各内角,F为△BDE内一点,BF、EF、DF分别平分△BDE各内角.若∠BFE的度数为整数,则∠BFE至少是113°度.
如图,△ABC内一点D,AD、BD、CD分别平分∠A、∠B、∠C,又E是△ABD内一点,AE、BE、CE分别平分△ABD各内角,F为△BDE内一点,BF、EF、DF分别平分△BDE各内角.若∠BFE的度数为整数,则∠BFE至少是113°度.