题目内容
11.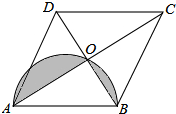 如图,菱形ABCD的对角线相交于点O,AC=8,BD=6,以AB为直径作一个半圆,则图中阴影部分的面积为$\frac{25}{8}$π-6.
如图,菱形ABCD的对角线相交于点O,AC=8,BD=6,以AB为直径作一个半圆,则图中阴影部分的面积为$\frac{25}{8}$π-6.
分析 首先根据菱形的性质,求出AO、BO的值是多少,再根据勾股定理,求出AB的值是多少;然后根据圆的面积公式,求出以AB为直径的半圆的面积,再用它减去三角形ABO的面积,求出图中阴影部分的面积为多少即可.
解答 解:∵AC=8,BD=6,AC⊥BD,
∴AB=$\sqrt{A{O}^{2}+B{O}^{2}}$=$\sqrt{{4}^{2}+{3}^{2}}$=5
∴图中阴影部分的面积为:
π×($\frac{5}{2}$)2×$\frac{1}{2}$-(8÷2)×(6÷2)÷2
=π×$\frac{25}{8}$-4×3÷2
=$\frac{25}{8}$π-6.
故答案为:$\frac{25}{8}$π-6.
点评 此题主要考查了菱形的性质,以及三角形、圆的面积的求法,要熟练掌握.

练习册系列答案
相关题目
16.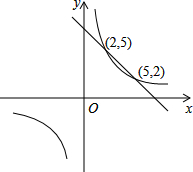 已知,如图一次函数y1=ax+b与反比例函数y2=$\frac{k}{x}$的图象如图示,当y1<y2时,x的取值范围是( )
已知,如图一次函数y1=ax+b与反比例函数y2=$\frac{k}{x}$的图象如图示,当y1<y2时,x的取值范围是( )
 已知,如图一次函数y1=ax+b与反比例函数y2=$\frac{k}{x}$的图象如图示,当y1<y2时,x的取值范围是( )
已知,如图一次函数y1=ax+b与反比例函数y2=$\frac{k}{x}$的图象如图示,当y1<y2时,x的取值范围是( )| A. | x<2 | B. | x>5 | C. | 2<x<5 | D. | 0<x<2或x>5 |
1.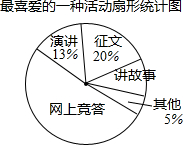 近期,我市中小学广泛开展了“传承中华文化,共筑精神家园”爱国主义读书教育活动,某中学为了解学生最喜爱的活动形式,以“我最喜爱的一种活动”为主题,进行随机抽样调查,收集数据整理后,绘制出以下两幅不完整的统计图表,请根据图中提供的信息,解答下面的问题:
近期,我市中小学广泛开展了“传承中华文化,共筑精神家园”爱国主义读书教育活动,某中学为了解学生最喜爱的活动形式,以“我最喜爱的一种活动”为主题,进行随机抽样调查,收集数据整理后,绘制出以下两幅不完整的统计图表,请根据图中提供的信息,解答下面的问题:
最喜爱的一种活动统计表
(1)在这次抽样调查中,一共调查了多少名学生?扇形统计图中“讲故事”部分的圆心角是多少度?
(2)如果这所中学共有学生3800名,那么请你估计最喜爱征文活动的学生人数.
 近期,我市中小学广泛开展了“传承中华文化,共筑精神家园”爱国主义读书教育活动,某中学为了解学生最喜爱的活动形式,以“我最喜爱的一种活动”为主题,进行随机抽样调查,收集数据整理后,绘制出以下两幅不完整的统计图表,请根据图中提供的信息,解答下面的问题:
近期,我市中小学广泛开展了“传承中华文化,共筑精神家园”爱国主义读书教育活动,某中学为了解学生最喜爱的活动形式,以“我最喜爱的一种活动”为主题,进行随机抽样调查,收集数据整理后,绘制出以下两幅不完整的统计图表,请根据图中提供的信息,解答下面的问题:最喜爱的一种活动统计表
| 活动形式 | 征文 | 讲故事 | 演讲 | 网上竞答 | 其他 |
| 人数 | 60 | 30 | 39 | a | b |
(2)如果这所中学共有学生3800名,那么请你估计最喜爱征文活动的学生人数.
 如图,边长为1的正方形ABCD一边AD在x负半轴上,直线l:y=$\frac{1}{2}$x+2经过点
如图,边长为1的正方形ABCD一边AD在x负半轴上,直线l:y=$\frac{1}{2}$x+2经过点
