题目内容
2.(1)解不等式组:$\left\{\begin{array}{l}{3x+1≤2(x+1),①}\\{\frac{x+1}{2}≥-1.①}\end{array}\right.$(2)先化简($\frac{x}{x-3}$-$\frac{x}{3-x}$)÷$\frac{2x}{{x}^{2}-9}$,然后选取一个你认为符合题意的x的值代入求值.
分析 (1)分别解两个不等式得到x≤1和x≥-3,然后根据大于小的小于大的取中间确定不等式组的解集;
(2)先进行括号的加法运算和除法运算化为乘法运算,然后约分得到原式=x+3,再根据分式有意义的条件取x=10代入计算即可.
解答 解:(1)解①得x≤1,
解②得x≥-3,
所以不等式组的解集为-3≤x≤1;
(2)原式=$\frac{x+x}{x-3}$•$\frac{(x+3)(x-3)}{2x}$
=x+3,
当x=10时,原式=10+3=13.
点评 本题考查了分式的化简求值:先把分式化简后,再把分式中未知数对应的值代入求出分式的值.在化简的过程中要注意运算顺序和分式的化简.化简的最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式.也考查了解不等式组.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.下列计算正确的是( )
| A. | -3÷3×3=-3 | B. | -3-3=0 | C. | -3-(-3)=-6 | D. | -3÷3÷3=-3 |
13.函数$y=\frac{x}{{\sqrt{x+3}}}$的自变量取值范围是( )
| A. | x≠0 | B. | x>-3 | C. | x≥-3且x≠0 | D. | x>-3且x≠0 |
14.某校九年级(1)班全体学生2016年初中毕业体育考试的成绩统计如表:
根据表中的信息判断,下列结论中错误的是( )
| 成绩(分) | 35 | 39 | 42 | 44 | 45 | 48 | 50 |
| 人数(人) | 2 | 5 | 6 | 6 | 8 | 7 | 6 |
| A. | 该班一共有40名同学 | |
| B. | 该班学生这次考试成绩的众数是45分 | |
| C. | 该班学生这次考试成绩的中位数是45分 | |
| D. | 该班学生这次考试成绩的平均数是45分 |
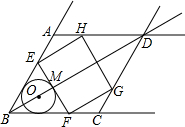 如图,在射线BA,BC,AD,CD围成的菱形ABCD中,∠ABC=60°,AB=6$\sqrt{3}$,O是射线BD上一点,⊙O与BA,BC都相切,与BO的延长线交于点M.过M作EF⊥BD交线段BA(或射线AD)于点E,交线段BC(或射线CD)于点F.以EF为边作矩形EFGH,点G,H分别在围成菱形的另外两条射线上.
如图,在射线BA,BC,AD,CD围成的菱形ABCD中,∠ABC=60°,AB=6$\sqrt{3}$,O是射线BD上一点,⊙O与BA,BC都相切,与BO的延长线交于点M.过M作EF⊥BD交线段BA(或射线AD)于点E,交线段BC(或射线CD)于点F.以EF为边作矩形EFGH,点G,H分别在围成菱形的另外两条射线上.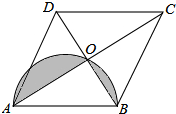 如图,菱形ABCD的对角线相交于点O,AC=8,BD=6,以AB为直径作一个半圆,则图中阴影部分的面积为$\frac{25}{8}$π-6.
如图,菱形ABCD的对角线相交于点O,AC=8,BD=6,以AB为直径作一个半圆,则图中阴影部分的面积为$\frac{25}{8}$π-6. 如图,将矩形纸片ABCD(AD>AB)折叠,使点C刚好落在线段AD上,且折痕分别与边BC,AD相交,设折叠后点C,D的对应点分别为点G,H,折痕分别与边BC,AD相交于点E,F.
如图,将矩形纸片ABCD(AD>AB)折叠,使点C刚好落在线段AD上,且折痕分别与边BC,AD相交,设折叠后点C,D的对应点分别为点G,H,折痕分别与边BC,AD相交于点E,F.