��Ŀ����
15��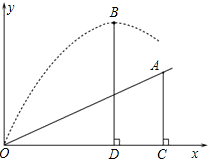 ��ͼ��С����һ�θ߶��������У���ɽ����O����һ������A���ȥ����ķ���·��Ϊ�����ߣ���������ǿ�������������������ֱ�߶�12��ʱ�����ƶ���ˮƽ����Ϊ9�ף���֪ɽ��OA��ˮƽ����OC�ļн�Ϊ30�㣬O��A�������$\frac{12}{5}$�ף�����ͼ��������ƽ��ֱ������ϵ��
��ͼ��С����һ�θ߶��������У���ɽ����O����һ������A���ȥ����ķ���·��Ϊ�����ߣ���������ǿ�������������������ֱ�߶�12��ʱ�����ƶ���ˮƽ����Ϊ9�ף���֪ɽ��OA��ˮƽ����OC�ļн�Ϊ30�㣬O��A�������$\frac{12}{5}$�ף�����ͼ��������ƽ��ֱ������ϵ����1��ֱ��д����A������
��2�������ķ���·�����������ߵĽ���ʽ
��3��ֱ���ж�С����һ���ܷ�Ѹ߶������O��ֱ�Ӵ�����A�㣮
���� ��1������30�����Ե�ֱ�DZ���б�ߵ�һ�����AC���ٸ��ݹ��ɶ�����OC��д����A�����ꣻ
��2�����ݶ��������ԭ����������ߵĽ���ʽ��
��3���ѵ�A�ĺ�������������ߵĽ���ʽ�У����yֵ��$\frac{6}{5}$��ȣ����ܽ���A�㣻�����ܴ�����A�㣮
��� �⣺��1����Rt��AOC�У��ߡ�AOC=30�㣬OA=$\frac{12}{5}$��
��AC=$\frac{6}{5}$��
�ɹ��ɶ����ã�OC=$\sqrt{O{A}^{2}-A{C}^{2}}$=$\sqrt{��\frac{12}{5}��^{2}-��\frac{6}{5}��^{2}}$=$\frac{6\sqrt{3}}{5}$��
��A��$\frac{6\sqrt{3}}{5}$��$\frac{6}{5}$����
��2��������ã�����B��9��12�����������߹�ԭ�㣬
�����������ߵĽ���ʽΪ��y=a��x-9��2+12��
�ѣ�0��0������ã�0=a��0-9��2+12��
a=-$\frac{4}{27}$��
����ķ���·�����������ߵĽ���ʽΪ��y=-$\frac{4}{27}$��x-9��2+12��
��3����x=$\frac{6\sqrt{3}}{5}$ʱ��y=-$\frac{4}{27}$��$\frac{6\sqrt{3}}{5}$-9��2+12��$\frac{6}{5}$��
��С����һ�˲��ܰѸ߶������O��ֱ�Ӵ�����A�㣮
���� �����Ƕ��κ�����Ӧ�ã����������ô���ϵ��������κ����Ľ���ʽ���뼸���е�ֱ����������30������Ե�ֱ�DZ���б�ߵ�һ�����ϣ������ù��ɶ�����߳�����ʾ������ꣻ�����жϸõ��Ƿ����������ϣ�

 ��ͼ��ʾ����֪������y=-x2+bx+c��x���һ������ΪA��4��0������y�ύ�ڵ�B��0��3�����������������Ӧ�ĺ�����ϵʽ��
��ͼ��ʾ����֪������y=-x2+bx+c��x���һ������ΪA��4��0������y�ύ�ڵ�B��0��3�����������������Ӧ�ĺ�����ϵʽ��
 ��ͼ��������y1=a��x-h��2��ֱ��y2=kx+b����A��0��-1����B��1��0�����㣮
��ͼ��������y1=a��x-h��2��ֱ��y2=kx+b����A��0��-1����B��1��0�����㣮