题目内容
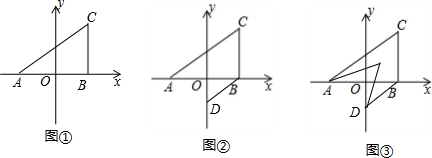
3.如图①,在平面直角坐标系中,点A、B在x轴上,AB⊥BC,AO=OB=2,BC=3(1)写出点A、B、C的坐标.
(2)如图②,过点B作BD∥AC交y轴于点D,求∠CAB+∠BDO的大小.
(3)如图③,在图②中,作AE、DE分别平分∠CAB、∠ODB,求∠AED的度数.
分析 (1)根据图形直接写出答案;
(2)根据两直线平行,内错角相等可得∠ABD=∠CAB,则∠CAB+∠BDO=∠ABD+∠BDO=90°;
(3)根据角平分线的定义可得∠CAE+∠BDE,过点E作EF∥AC,然后根据平行线的性质求出∠AED=∠CAE+∠BDE.
解答 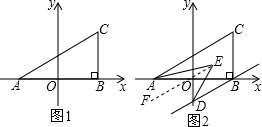 解:(1)依题意得:A(-2,0),B(2,0),C(2,3);
解:(1)依题意得:A(-2,0),B(2,0),C(2,3);
(2)∵BD∥AC,
∴∠ABD=∠BAC,
∴CAB+∠BDO=∠ABD+∠BDO=90°;
(3):∵BD∥AC,
∴∠ABD=∠BAC,
∵AE,DE分别平分∠CAB,∠ODB,
∴∠CAE+∠BDE=$\frac{1}{2}$(∠BAC+∠BDO)=$\frac{1}{2}$(∠ABD+∠BDO)=$\frac{1}{2}$×90°=45°,
过点E作EF∥AC,
则∠CAE=∠AEF,∠BDE=∠DEF,
∴∠AED=∠AEF+∠DEF=∠CAE+∠BDE=45°.
点评 本题考查了坐标与图形性质,平行线的性质,三角形的面积,熟记性质并求出点A、B、C的坐标是解题的关键,(3)作出平行线是解题的关键.

练习册系列答案
相关题目
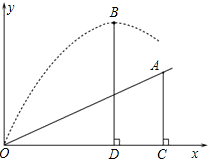 如图,小明在一次高尔夫球赛中,从山坡下O点打出一球向球洞A点飞去,球的飞行路线为抛物线.如果不考虑空气阻力,当球打到最大竖直高度12米时,球移动的水平距离为9米.已知山坡OA与水平方向OC的夹角为30°,O、A两点相距$\frac{12}{5}$米.在如图所建立的平面直角坐标系下
如图,小明在一次高尔夫球赛中,从山坡下O点打出一球向球洞A点飞去,球的飞行路线为抛物线.如果不考虑空气阻力,当球打到最大竖直高度12米时,球移动的水平距离为9米.已知山坡OA与水平方向OC的夹角为30°,O、A两点相距$\frac{12}{5}$米.在如图所建立的平面直角坐标系下