题目内容
7．
如图所示，已知抛物线y=-x2+bx+c与x轴的一个交点为A（4，0），与y轴交于点B（0，3）．求此抛物线所对应的函数关系式．
分析 直接利用待定系数法求出二次函数解析式进而得出答案．
解答 解：把点A（4，0），B（0，3）代入二次函数y=-x2+bx+c，
$\left\{\begin{array}{l}{c=3}\\{-16+4b+c=0}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{b=\frac{13}{4}}\\{c=3}\end{array}\right.$，
所以二次函数的关系式为：y=-x2+$\frac{13}{4}$x+3．
点评 此题主要考查了待定系数法求函数解析式，正确将点代入函数解析式是解题关键．
练习册系列答案
相关题目
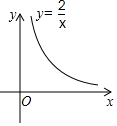已知点A（1，y1），B（2，y2）是如图所示的反比例函数y=$\frac{2}{x}$图象上两点，则y1＞y2（填“＞”，“＜”或“=”）．
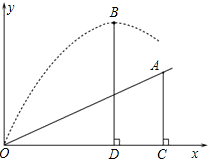如图，小明在一次高尔夫球赛中，从山坡下O点打出一球向球洞A点飞去，球的飞行路线为抛物线．如果不考虑空气阻力，当球打到最大竖直高度12米时，球移动的水平距离为9米．已知山坡OA与水平方向OC的夹角为30°，O、A两点相距$\frac{12}{5}$米．在如图所建立的平面直角坐标系下
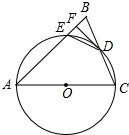如图，在△ABC中，AB=AC，以AC为直径的⊙O交BC于点D，交AB于点E，过点D作DF⊥AB，垂足为F，连接DE．