题目内容
4.山坡上有一棵与水平面垂直的大树,一场台风过后,大树被刮倾斜后折断倒在山坡上,树的顶部恰好接触到坡面(如图所示).已知山坡的坡角∠AEF=23°,量得树干倾斜角∠BAC=38°,大树被折断部分和坡面所成的角∠ADC=60°,AD=4m.
(1)求∠DAC的度数;
(2)求这棵大树折点C到坡面AE的距离.(结果精确到个位,参考数据:$\sqrt{2}$=1.4,$\sqrt{3}$=1.7,$\sqrt{6}$=2.4)
分析 (1)通过延长BA交EF于一点M,则∠CAD=180°-∠BAC-∠EAM即可求得;
(2)作AH⊥CD于H点,作CG⊥AE于G点,先求得CD的长,然后再求得CG的长.
解答 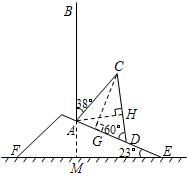 解:(1)延长BA交EF于点M.
解:(1)延长BA交EF于点M.
在Rt△AME中,∠E=23°,
∴∠MAE=67°.
又∵∠BAC=38°,
∴∠DAC=180°-67°-38°=75°;
(2)作AH⊥CD于H点,作CG⊥AE于G点.
在△ADH中,∠ADC=60°,AD=4,cos∠ADC=$\frac{DH}{AD}$,
∴DH=2.
sin∠ADC=$\frac{AH}{AD}$,
∴AH=2$\sqrt{3}$.
在Rt△ACH中,∠C=180°-75°-60°=45°,
∴CH=AH=2$\sqrt{3}$.
∴CD=DH+CH=2$\sqrt{3}$.
在Rt△CDG中,∠CDG=60°,sin∠CDG=$\frac{CG}{CD}$,∴CG=3+$\sqrt{3}$≈5米.
答:折点C距离坡面AE约为5米.
点评 本题主要考查学生对坡度坡角的掌握及三角函数的运用能力,但综合性较强,有一定的复杂性.

练习册系列答案
 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
14.某社区准备在甲乙两位射箭爱好者中选出一人参加集训,两人各射了5箭,他们的总成绩(单位:环)相同.
(1)a=4,$\overline{{x}_{乙}}$=6;
(2)①分别计算甲、乙成绩的方差.
②请你从平均数和方差的角度分析,谁将被选中.
| 第1次 | 第2次 | 第3次 | 第4次 | 第5次 | |
| 甲成绩 | 9 | 4 | 7 | 4 | 6 |
| 乙成绩 | 7 | 5 | 7 | a | 7 |
(2)①分别计算甲、乙成绩的方差.
②请你从平均数和方差的角度分析,谁将被选中.
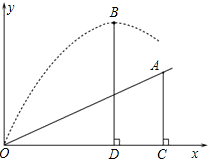 如图,小明在一次高尔夫球赛中,从山坡下O点打出一球向球洞A点飞去,球的飞行路线为抛物线.如果不考虑空气阻力,当球打到最大竖直高度12米时,球移动的水平距离为9米.已知山坡OA与水平方向OC的夹角为30°,O、A两点相距$\frac{12}{5}$米.在如图所建立的平面直角坐标系下
如图,小明在一次高尔夫球赛中,从山坡下O点打出一球向球洞A点飞去,球的飞行路线为抛物线.如果不考虑空气阻力,当球打到最大竖直高度12米时,球移动的水平距离为9米.已知山坡OA与水平方向OC的夹角为30°,O、A两点相距$\frac{12}{5}$米.在如图所建立的平面直角坐标系下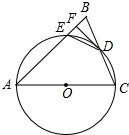 如图,在△ABC中,AB=AC,以AC为直径的⊙O交BC于点D,交AB于点E,过点D作DF⊥AB,垂足为F,连接DE.
如图,在△ABC中,AB=AC,以AC为直径的⊙O交BC于点D,交AB于点E,过点D作DF⊥AB,垂足为F,连接DE. 如图,E为△ABC的边BC上一点,D在BA的延长线上,DE交AC于点F,∠B=45°,∠C=30°,∠EFC=70°,求∠D的度数.
如图,E为△ABC的边BC上一点,D在BA的延长线上,DE交AC于点F,∠B=45°,∠C=30°,∠EFC=70°,求∠D的度数.