题目内容
15.方程x2-2x=$\frac{1}{x}$-2实数根的情况是( )| A. | 有三个实数根 | B. | 有两个实数根 | C. | 有一个实数根 | D. | 无实数根 |
分析 将方程变形为:$\frac{1}{x}$-1=(x-1)2,设y1=$\frac{1}{x}$-1,y2=(x-1)2,在坐标系中画出两个函数的图象,看其交点个数即可.
解答  解:将方程变形$\frac{1}{x}$-1=(x-1)2,
解:将方程变形$\frac{1}{x}$-1=(x-1)2,
设y1=$\frac{1}{x}$-1,y2=(x-1)2,在坐标系中画出两个函数的图象如图所示:
可看出两个函数有一个交点(1,0).
故方程x2-2x=$\frac{1}{x}$-2有一个实数根.
故选C.
点评 本题考查了抛物线与x轴的交点.解答该题时采用了“数形结合”的数学思想,减少了解题过程中的繁琐的计算.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
5.下列运算正确的是( )
| A. | -a2+2a2=3a2 | B. | 3a2×(-2a)=-6a2 | C. | a8÷a4=a2 | D. | (2a2)2=4a4 |
3.学校买来钢笔若干枝,可以平均分给(x-1)名同学,也可分给(x-2)名同学(x为正整数).用代数式表示钢笔的数量不可能的是( )
| A. | x2+3x+2 | B. | 3(x-1)(x-2) | C. | x2-3x+2 | D. | x3-3x2+2x |
10.下列计算正确的是( )
| A. | $\sqrt{(-2)^{2}}$=-2 | B. | (a2)5=a10 | C. | a2+a5=a7 | D. | 6$\sqrt{5}$×2$\sqrt{5}$=12$\sqrt{5}$ |
4.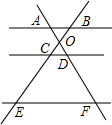 如图,已知AB∥CD∥EF,直线AF与直线BE相交于点O,下列结论错误的是( )
如图,已知AB∥CD∥EF,直线AF与直线BE相交于点O,下列结论错误的是( )
 如图,已知AB∥CD∥EF,直线AF与直线BE相交于点O,下列结论错误的是( )
如图,已知AB∥CD∥EF,直线AF与直线BE相交于点O,下列结论错误的是( )| A. | $\frac{AD}{DF}=\frac{BC}{CE}$ | B. | $\frac{OA}{OC}=\frac{OB}{OD}$ | C. | $\frac{CD}{EF}=\frac{OC}{OE}$ | D. | $\frac{OA}{OF}=\frac{OB}{OE}$ |
 如图,网格中的四个格点组成菱形ABCD,则tan∠DBC的值为3.
如图,网格中的四个格点组成菱形ABCD,则tan∠DBC的值为3. 如图,这个二次函数图象的表达式可能是y=x2-x.(只写出一个)
如图,这个二次函数图象的表达式可能是y=x2-x.(只写出一个)