题目内容
10.下列计算正确的是( )| A. | $\sqrt{(-2)^{2}}$=-2 | B. | (a2)5=a10 | C. | a2+a5=a7 | D. | 6$\sqrt{5}$×2$\sqrt{5}$=12$\sqrt{5}$ |
分析 A:根据算术平方根的求法判断即可.
B:根据幂的乘方的运算方法计算即可.
C:根据整式加法的运算方法判断即可.
D:根据二次根式的乘方运算方法计算即可.
解答 解:∵$\sqrt{{(-2)}^{2}}=2$,
∴选项A不正确;
∵(a2)5=a10,
∴选项B正确;
∵a2+a5≠a7,
∴选项C不正确;
∵6$\sqrt{5}$×2$\sqrt{5}$=60,
∴选项D不正确;
故选:B.
点评 (1)此题主要考查了幂的乘方和积的乘方,要熟练掌握,解答此题的关键是要明确:①(am)n=amn(m,n是正整数);②(ab)n=anbn(n是正整数).
(2)此题还考查了二次根式的乘除法,要熟练掌握,解答此题的关键是要明确:①积的算术平方根性质:a•b=a•b(a≥0,b≥0);②二次根式的乘法法则:a•b=a•b(a≥0,b≥0);③商的算术平方根的性质:ab=ab(a≥0,b>0);④二次根式的除法法则:ab=ab(a≥0,b>0).
(3)此题还考查了合并同类项的方法,以及二次根式的性质和化简,要熟练掌握.

练习册系列答案
相关题目
15.方程x2-2x=$\frac{1}{x}$-2实数根的情况是( )
| A. | 有三个实数根 | B. | 有两个实数根 | C. | 有一个实数根 | D. | 无实数根 |
 如图,在等边三角形ABC中,点E、F分别是AB、AC的中点,EF=4,△ABC的周长为24.
如图,在等边三角形ABC中,点E、F分别是AB、AC的中点,EF=4,△ABC的周长为24. 如图,抛物线y=-x2+6x交x轴正半轴于点A,顶点为M,对称轴MB交x轴于点B.过点C(2,0)作射线CD交MB于点D(D在x轴上方),OE∥CD交MB于点E,EF∥x轴交CD于点F,作直线MF.
如图,抛物线y=-x2+6x交x轴正半轴于点A,顶点为M,对称轴MB交x轴于点B.过点C(2,0)作射线CD交MB于点D(D在x轴上方),OE∥CD交MB于点E,EF∥x轴交CD于点F,作直线MF.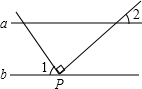 如图,直线a∥b,直角三角板的直角顶点P在直线b上,若∠1=56°,则∠2的度数34°.
如图,直线a∥b,直角三角板的直角顶点P在直线b上,若∠1=56°,则∠2的度数34°.