题目内容
4.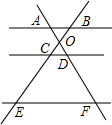 如图,已知AB∥CD∥EF,直线AF与直线BE相交于点O,下列结论错误的是( )
如图,已知AB∥CD∥EF,直线AF与直线BE相交于点O,下列结论错误的是( )| A. | $\frac{AD}{DF}=\frac{BC}{CE}$ | B. | $\frac{OA}{OC}=\frac{OB}{OD}$ | C. | $\frac{CD}{EF}=\frac{OC}{OE}$ | D. | $\frac{OA}{OF}=\frac{OB}{OE}$ |
分析 根据平行线分线段成比例定理,由AB∥CD∥EF可对A选项进行判断;由AB∥CD可对B选项进行判断;根据平行于三角形的一边,并且和其他两边(或两边的延长线)相交的直线,所截得的三角形的三边与原三角形的三边对应成比例,由CD∥EF可对C选项进行判断;根据平行线分线段成比例定理,由AB∥EF可对D选项进行判断.
解答 解:A、由AB∥CD∥EF,则$\frac{AD}{DF}$=$\frac{BC}{CE}$,所以A选项的结论正确;
B、由AB∥CD,则$\frac{OA}{OD}$=$\frac{OB}{OC}$,所以B选项的结论错误;
C、由CD∥EF,则$\frac{CD}{EF}$=$\frac{OC}{OE}$,所以C选项的结论正确;
D、由AB∥EF,则$\frac{OA}{OF}$=$\frac{OB}{OE}$,所以D选项的结论正确.
故选B.
点评 本题考查了平行线分线段成比例定理:三条平行线截两条直线,所得的对应线段成比例.平行于三角形的一边,并且和其他两边(或两边的延长线)相交的直线,所截得的三角形的三边与原三角形的三边对应成比例.

练习册系列答案
相关题目
15.方程x2-2x=$\frac{1}{x}$-2实数根的情况是( )
| A. | 有三个实数根 | B. | 有两个实数根 | C. | 有一个实数根 | D. | 无实数根 |
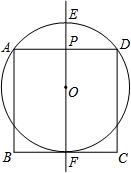 在正方形ABCD中,AD=2,l是过AD中点P的一条直线.O是l上一点,以O为圆心的圆经过点A、D,直线l与⊙O交于点E、F(E、F不与A、D重合,E在F的上面).
在正方形ABCD中,AD=2,l是过AD中点P的一条直线.O是l上一点,以O为圆心的圆经过点A、D,直线l与⊙O交于点E、F(E、F不与A、D重合,E在F的上面).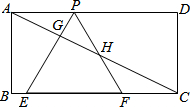 如图,已知矩形ABCD,AB=$\sqrt{3}$,BC=3,在BC上取两点E,F(E在F左边),以EF为边作等边三角形PEF,使顶点P在AD上,PE,PF分别交AC于点G,H.
如图,已知矩形ABCD,AB=$\sqrt{3}$,BC=3,在BC上取两点E,F(E在F左边),以EF为边作等边三角形PEF,使顶点P在AD上,PE,PF分别交AC于点G,H.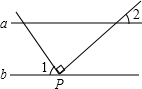 如图,直线a∥b,直角三角板的直角顶点P在直线b上,若∠1=56°,则∠2的度数34°.
如图,直线a∥b,直角三角板的直角顶点P在直线b上,若∠1=56°,则∠2的度数34°.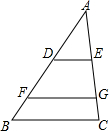 如图,△ABC中,D、F在AB边上,E、G在AC边上,DE∥FG∥BC,且AD:DF:FB=3:2:1,若AG=15,则CE的长为( )
如图,△ABC中,D、F在AB边上,E、G在AC边上,DE∥FG∥BC,且AD:DF:FB=3:2:1,若AG=15,则CE的长为( )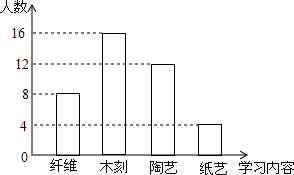 某校初二学年学生即将参加劳动实践基地的学习活动,为了解学生对学习内容的喜爱情况,学校决定围绕“纸艺、木刻、陶艺、纤维四项学习内容中,你参加哪一项(每人必选且只选一项)的问题”,在全学年范围内随机抽取部分学生进行问卷调查,并将调查结果绘制成如图所示的条形统计图,请根据图中提供的信息解答下列问题:
某校初二学年学生即将参加劳动实践基地的学习活动,为了解学生对学习内容的喜爱情况,学校决定围绕“纸艺、木刻、陶艺、纤维四项学习内容中,你参加哪一项(每人必选且只选一项)的问题”,在全学年范围内随机抽取部分学生进行问卷调查,并将调查结果绘制成如图所示的条形统计图,请根据图中提供的信息解答下列问题: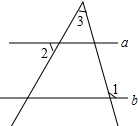 如图,直线a∥b,∠1=110°,∠2=55°,则∠3的度数为55°.
如图,直线a∥b,∠1=110°,∠2=55°,则∠3的度数为55°.