题目内容
已知抛物线y=-x2+2mx-3经过点M(5,-8),并与x轴交于A,B两点(点A在点B的左边).
(1)求抛物线的顶点坐标;
(2)在抛物线上是否存在点P,使△ABP的面积为3?若存在,求出满足条件的点P的坐标;若不存在,请说明理由.
(1)求抛物线的顶点坐标;
(2)在抛物线上是否存在点P,使△ABP的面积为3?若存在,求出满足条件的点P的坐标;若不存在,请说明理由.
考点:抛物线与x轴的交点
专题:
分析:(1)把M点坐标代入解析式可求得m,可求得抛物线的解析式,可求得其顶点坐标;
(2)由(1)可求得A、B坐标,由条件可求得P点的纵坐标,代入可求得P点的坐标.
(2)由(1)可求得A、B坐标,由条件可求得P点的纵坐标,代入可求得P点的坐标.
解答:解:
(1)∵抛物线y=-x2+2mx-3经过点M(5,-8),
∴-8=-25+10m-3,解得m=2,
∴抛物线解析式为y=-x2+4x-3=-(x-2)2+1,
∴其顶点坐标为(2,1);
(2)在y=-x2+4x-3中,令y=0可得-x2+4x-3=0,解得x=1或x=3,
∴A点为(1,0),B为(3,0),
∴AB=3-1=2,
设P点坐标为(x,y),
则S△ABP=
×2×|y|=3,
解得y=±3,
当y=3时,可得3=-x2+4x-3,其判别式△=16-24<0,该方程无实数根;
当y=-3时,可得-3=-x2+4x-3,解得x=0(舍去)或x=4,此时P点坐标为(-3,4);
综上可知存在满足条件的点P,其坐标为(-3,4).
(1)∵抛物线y=-x2+2mx-3经过点M(5,-8),
∴-8=-25+10m-3,解得m=2,
∴抛物线解析式为y=-x2+4x-3=-(x-2)2+1,
∴其顶点坐标为(2,1);
(2)在y=-x2+4x-3中,令y=0可得-x2+4x-3=0,解得x=1或x=3,
∴A点为(1,0),B为(3,0),
∴AB=3-1=2,
设P点坐标为(x,y),
则S△ABP=
| 1 |
| 2 |
解得y=±3,
当y=3时,可得3=-x2+4x-3,其判别式△=16-24<0,该方程无实数根;
当y=-3时,可得-3=-x2+4x-3,解得x=0(舍去)或x=4,此时P点坐标为(-3,4);
综上可知存在满足条件的点P,其坐标为(-3,4).
点评:本题主要考查待定系数法求函数解析式和函数与x轴的交点坐标,在(1)中求得m的值是解题的关键,在(2)中求得P的纵坐标是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列方程式中,有解的是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
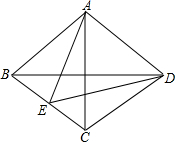 如图,在菱形ABCD中,点E在BC上,若∠ABC=∠EAD=70°,则∠CED的度数是( )
如图,在菱形ABCD中,点E在BC上,若∠ABC=∠EAD=70°,则∠CED的度数是( )| A、70° | B、60° |
| C、55° | D、50° |
 如图,直线l是四边形ABCD的对称轴,若AB=CD,有下面的结论:①AB⊥BC;②AC⊥BD;③AB∥CD;④AO=OC.其中正确的结论有
如图,直线l是四边形ABCD的对称轴,若AB=CD,有下面的结论:①AB⊥BC;②AC⊥BD;③AB∥CD;④AO=OC.其中正确的结论有 如图,在△ABC中,AD、AE分别是边BC上的中线和高,AE=2cm,S△ABD=3cm2,求BC和DC的长.
如图,在△ABC中,AD、AE分别是边BC上的中线和高,AE=2cm,S△ABD=3cm2,求BC和DC的长.