题目内容
若解关于x的方程
-3=
无解,求代数式(
-
)•(a2-1)的值.
| 1 |
| x-5 |
| x-a |
| 5-x |
| 2 |
| a-1 |
| 1 |
| a+1 |
考点:分式方程的解,分式的化简求值
专题:
分析:先将分式方程化为整式方程,用含x的式子表示a的值,然后根据分式方程无实数根,得出x的值,继而求出a的值,然后将a的值代入即可.
解答:解:方程
-3=
,
去分母化成整式方程得:2x+a-16=0,
所以a=16-2x,
因为关于x的方程
-3=
无解,
所以x=5,
所以a=16-2×5=6,
当a=6时,
(
-
)•(a2-1)
=
•(a2-1)
=2(a+1)-(a-1)
=a+3
=6+3
=9.
| 1 |
| x-5 |
| x-a |
| 5-x |
去分母化成整式方程得:2x+a-16=0,
所以a=16-2x,
因为关于x的方程
| 1 |
| x-5 |
| x-a |
| 5-x |
所以x=5,
所以a=16-2×5=6,
当a=6时,
(
| 2 |
| a-1 |
| 1 |
| a+1 |
=
| 2(a+1)-(a-1) |
| a2-1 |
=2(a+1)-(a-1)
=a+3
=6+3
=9.
点评:本题考查分式方程的解,当无解时,就是有增根时,化成整式方程代入增根可求出a的值,然后将a的值代入即可.

练习册系列答案
相关题目
 如图,长方体的底面边长分别为2cm和4cm,高为5cm.若一只蚂蚁从P点开始经过4个侧面爬行一圈到达Q点,则蚂蚁爬行的最短路径长为( )
如图,长方体的底面边长分别为2cm和4cm,高为5cm.若一只蚂蚁从P点开始经过4个侧面爬行一圈到达Q点,则蚂蚁爬行的最短路径长为( )A、
| ||
| B、11cm | ||
| C、13cm | ||
| D、17cm |
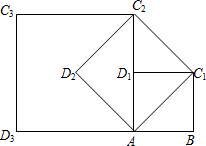 如图,在正方形ABC1D1中,AB=1.连接AC1,以AC1为边作第二个正方形AC1C2D2;连接AC2,以AC2为边作第三个正方形AC2C3D3.则
如图,在正方形ABC1D1中,AB=1.连接AC1,以AC1为边作第二个正方形AC1C2D2;连接AC2,以AC2为边作第三个正方形AC2C3D3.则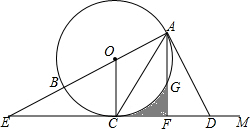 如图,AB是⊙O的直径,CM是⊙O的切线,切点为C,延长AB交CD于点E,连接AC,在射线CM上取一点D使DA=DC,作AF⊥ED于点F,交⊙O于点G,
如图,AB是⊙O的直径,CM是⊙O的切线,切点为C,延长AB交CD于点E,连接AC,在射线CM上取一点D使DA=DC,作AF⊥ED于点F,交⊙O于点G, 如图,在直角梯形ABCD中,BF=AE=DG=x,AB=6,CD=3,AD=4,则四边形CGEF的面积y与x之间的函数关系式为
如图,在直角梯形ABCD中,BF=AE=DG=x,AB=6,CD=3,AD=4,则四边形CGEF的面积y与x之间的函数关系式为