题目内容
14.在菱形ABCD中,AB=4,∠A=60°,E为AB的中点,若在线段BD上取一点P,则PA+PE的最小值是( )| A. | 2$\sqrt{3}$ | B. | 4 | C. | 2$\sqrt{5}$ | D. | 2$\sqrt{7}$ |
分析 如图,连接CE交BD于P,则PA+PE的最小值=CE,根据菱形的性质得到BC=AB=4,∠ABC=120°,由E为AB的中点,得到BE=$\frac{1}{2}$AB=2,过E作EF⊥BC交CB的延长线于F,得到∠FBE=60°,根据勾股定理即可得到结论.
解答 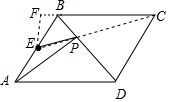 解:如图,连接CE交BD于P,则PA+PE的最小值=CE,
解:如图,连接CE交BD于P,则PA+PE的最小值=CE,
∵在菱形ABCD中,AB=4,∠A=60°,
∴BC=AB=4,∠ABC=120°,
∵E为AB的中点,
∴BE=$\frac{1}{2}$AB=2,
过E作EF⊥BC交CB的延长线于F,
∴∠FBE=60°,
∴BF=1,EF=$\sqrt{3}$,
∴CF=5,
∴CE=$\sqrt{C{F}^{2}+E{F}^{2}}$=2$\sqrt{7}$,
∴PA+PE的最小值是2$\sqrt{7}$,
故选D.
点评 本题考查了菱形的性质,轴对称的性质,难度适中,确定点P的位置是解题的关键.

练习册系列答案
相关题目
11.已知下列命题:①若x=0,则x2-2x=0;②若$\root{3}{a}$=$\root{3}{b}$,则a=b;③矩形既是轴对称图形又是中心对称图形;④圆内接四边形的对角一定相等.其中原命题与逆命题均为真命题的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
9.若正比例函数y=kx与反比例函数y=$\frac{{k}^{′}}{x}$的一个交点坐标为(-2,3),则另一个交点为( )
| A. | (-2,-3) | B. | (2,3) | C. | (2,-3) | D. | (3,2) |
19. 如图,在△ABC和△DEF中,AB=DE,∠B=∠DEF,补充下列哪一条件后,能应用“SAS”判定△ABC≌△DEF( )
如图,在△ABC和△DEF中,AB=DE,∠B=∠DEF,补充下列哪一条件后,能应用“SAS”判定△ABC≌△DEF( )
 如图,在△ABC和△DEF中,AB=DE,∠B=∠DEF,补充下列哪一条件后,能应用“SAS”判定△ABC≌△DEF( )
如图,在△ABC和△DEF中,AB=DE,∠B=∠DEF,补充下列哪一条件后,能应用“SAS”判定△ABC≌△DEF( )| A. | ∠A=∠D | B. | ∠ACB=∠DFE | C. | AC=DF | D. | BE=CF |
6.下列等式中成立的是( )
| A. | a4•a=a4 | B. | a6-a3=a3 | C. | (ab2)3=a3•b5 | D. | (a3)2=a6 |
4.已知点P在第四象限,且到x轴的距离是2,到y轴的距离是3,则点P的坐标为( )
| A. | (2,-3) | B. | (-3,2) | C. | (3,-2) | D. | (-2,3) |