题目内容
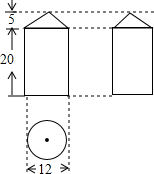如图是某几何体的三视图．（1）画出此几何体的示意图及表面展开图；
（2）计算出此几何体的表面积．（结果保留π）
考点：由三视图判断几何体,几何体的展开图
专题：
分析：（1）由三视图可知，该几何体由上部分是底面直径为12，高为5的圆锥和下部分是底面直径为12，高为20的圆柱组成；
（2）根据勾股定理求出圆锥母线长，再根据圆锥和圆柱的表面积公式求解即可．
（2）根据勾股定理求出圆锥母线长，再根据圆锥和圆柱的表面积公式求解即可．
解答：解：（1）由三视图可知，该几何体由上部分是底面直径为12，高为5的圆锥和下部分是底面直径为12，高为20的圆柱组成．
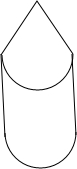
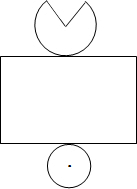
（2）圆锥，圆柱底面半径为r=6
由勾股定理得圆锥母线长为
=
，
圆锥侧面积=
π•12×
=6
π，
表面积=π•62+π•12×20+6
π=276π6
π．
（2）圆锥，圆柱底面半径为r=6
由勾股定理得圆锥母线长为
| 52+62 |
| 61 |
圆锥侧面积=
| 1 |
| 2 |
| 61 |
| 61 |
表面积=π•62+π•12×20+6
| 61 |
| 61 |
点评：考查由三视图判断几何体及几何体表面积的计算；得到几何体的形状是解决本题的突破点．
练习册系列答案
相关题目
已知，如图，在?ABCD中，E，F分别是BC，AD的中点，AE，BF相交于点G，DE，CF相交于点H，求证：GH∥AD且GH=
如图，△ABC内接于⊙O，BC=4，CA=3，∠A-∠B=90°，求⊙O的半径．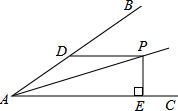
若∠BAC=30°，AP平分∠BAC，PD∥AC且PD=5，PE⊥AC于E，则PE=
如图，已知等腰△ABC内接于⊙O，AB=AC=5，BC=8，求点O到BC的距离．