题目内容
 如图,△ABC内接于⊙O,BC=4,CA=3,∠A-∠B=90°,求⊙O的半径.
如图,△ABC内接于⊙O,BC=4,CA=3,∠A-∠B=90°,求⊙O的半径.考点:圆周角定理,勾股定理
专题:计算题
分析:作直径BD,连结DC、DA,如图根据圆周角定理得∠BAD=∠BCD=90°,由于∠CAB-∠CBA=90°,可得到∠CAD=∠CBA,则可证出∠CAD=∠CDA,所以CA=CD=3,然后在Rt△BCD中根据勾股定理计算出BD,从而可得到圆的半径.
解答:解:作直径BD,连结DC、DA,如图,
∵BD为直径,
∴∠BAD=∠BCD=90°,
∵∠CAB-∠CBA=90°,
∴∠CAD=∠CBA,
而∠CBA=∠CDA,
∴∠CAD=∠CDA,
∴CA=CD=3,
在Rt△BCD中,∵BC=4,CD=3,
∴BD=
=5,
B∴⊙O的半径为
.

∵BD为直径,
∴∠BAD=∠BCD=90°,
∵∠CAB-∠CBA=90°,
∴∠CAD=∠CBA,
而∠CBA=∠CDA,
∴∠CAD=∠CDA,
∴CA=CD=3,
在Rt△BCD中,∵BC=4,CD=3,
∴BD=
| CD2+BC2 |
B∴⊙O的半径为
| 5 |
| 2 |
点评:本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.也考查了勾股定理.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
如图,下列选项中不是正六棱柱三视图的是( )
A、 |
B、 |
C、 |
D、 |
函数y=
的自变量x的取值范围是( )
| x-4 |
| A、x≠4 | B、x>4 |
| C、x≥4 | D、x≤4 |
 已知:如图,点B、F、C、E在一条直线上,∠A=∠D,AC=DF且AC∥DF
已知:如图,点B、F、C、E在一条直线上,∠A=∠D,AC=DF且AC∥DF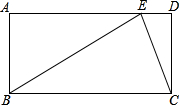 如图,矩形ABCD中,E是AD上一点,BC=BE=2CD,求∠DCE的度数.
如图,矩形ABCD中,E是AD上一点,BC=BE=2CD,求∠DCE的度数. △BCD中,BC=CD,∠BCD=90°,E是△BCD外一点,CE∥BD,且BE=BD,求
△BCD中,BC=CD,∠BCD=90°,E是△BCD外一点,CE∥BD,且BE=BD,求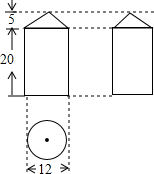 如图是某几何体的三视图.
如图是某几何体的三视图. 如图,A,B,C三点在同一直线上,△ADC,△BEC是等边三角形,连接AE,BD.求证:
如图,A,B,C三点在同一直线上,△ADC,△BEC是等边三角形,连接AE,BD.求证: