题目内容
 已知,如图,在?ABCD中,E,F分别是BC,AD的中点,AE,BF相交于点G,DE,CF相交于点H,求证:GH∥AD且GH=
已知,如图,在?ABCD中,E,F分别是BC,AD的中点,AE,BF相交于点G,DE,CF相交于点H,求证:GH∥AD且GH=| 1 |
| 2 |
考点:平行四边形的性质,三角形中位线定理
专题:证明题
分析:连接EF,可分别证明四边形ABEF和CDFE为平行四边形,可得G、H分别为BF、CF的中点,利用三角形中位线定理可证得结论.
解答: 证明:
证明:
如图,连接EF,
∵四边形ABCD为平行四边形,
∴AD∥BC,且AD=BC,
∵E、F分别为AD、BC中点,
∴AF=BE,且AF∥BE,
∴四边形ABEF为平行四边形,
∴G为BF中点,
同理可证明H为FC中点,
∴GH为△BCF的中位线,
∴GH∥AD且GH=
AD.
 证明:
证明:如图,连接EF,
∵四边形ABCD为平行四边形,
∴AD∥BC,且AD=BC,
∵E、F分别为AD、BC中点,
∴AF=BE,且AF∥BE,
∴四边形ABEF为平行四边形,
∴G为BF中点,
同理可证明H为FC中点,
∴GH为△BCF的中位线,
∴GH∥AD且GH=
| 1 |
| 2 |
点评:本题主要考查平行四边形的判定和性质,掌握平行四边形的判定和性质是解题的关键,即①两组对边分别平行的四边形?平行四边形,②两组对边分别相等的四边形?平行四边形,③一组对边平行且相等的四边形?平行四边形,④两组对角分别相等的四边形?平行四边形,⑤对角线互相平分的四边形?平行四边形.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案
相关题目
 如图,三条直线l1,l2,l3相交于点E,则∠1+∠2+∠3=( )
如图,三条直线l1,l2,l3相交于点E,则∠1+∠2+∠3=( )| A、360° | B、180° |
| C、120° | D、90° |
函数y=
中自变量x的取值范围是( )
| 2x-1 |
A、x≥-
| ||
B、x≥
| ||
| C、x≤-2 | ||
| D、x≤2 |
 已知如图,在菱形ABCD中,AC,BD相交于点O,在图中有几个直角三角形?分别是哪些?
已知如图,在菱形ABCD中,AC,BD相交于点O,在图中有几个直角三角形?分别是哪些?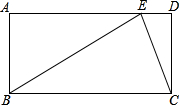 如图,矩形ABCD中,E是AD上一点,BC=BE=2CD,求∠DCE的度数.
如图,矩形ABCD中,E是AD上一点,BC=BE=2CD,求∠DCE的度数.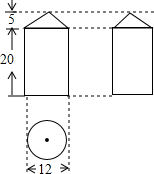 如图是某几何体的三视图.
如图是某几何体的三视图.