题目内容
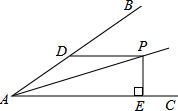 若∠BAC=30°,AP平分∠BAC,PD∥AC且PD=5,PE⊥AC于E,则PE=
若∠BAC=30°,AP平分∠BAC,PD∥AC且PD=5,PE⊥AC于E,则PE=考点:含30度角的直角三角形,角平分线的性质
专题:
分析:过P作PF⊥AB于F,根据平行线的性质可得∠FDP=∠BAC=30°,再根据30度所对的边是斜边的一半可求得PF的长,最后根据角平分线的性质即可求得PE的长.
解答: 解:过P作PF⊥AB于F,
解:过P作PF⊥AB于F,
∵PD∥AC,
∴∠FDP=∠BAC=30°,
∴在Rt△PDF中,PF=
PD=2.5,
∵AP平分∠BAC,PE⊥AC于E,PF⊥AB于F,
∴PE=PF=2.5.
故答案为2.5.
 解:过P作PF⊥AB于F,
解:过P作PF⊥AB于F,∵PD∥AC,
∴∠FDP=∠BAC=30°,
∴在Rt△PDF中,PF=
| 1 |
| 2 |
∵AP平分∠BAC,PE⊥AC于E,PF⊥AB于F,
∴PE=PF=2.5.
故答案为2.5.
点评:本题考查了角平分线的性质,直角三角形30°角所对的直角边等于斜边的一半的性质,平行线的性质,熟记性质是解题的关键.

练习册系列答案
相关题目
 如图,AC⊥BD,AC=DC,BC=EC,连接DE并延长交AB于F,求证:DF⊥AB.
如图,AC⊥BD,AC=DC,BC=EC,连接DE并延长交AB于F,求证:DF⊥AB.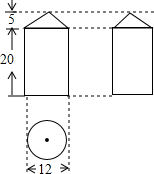 如图是某几何体的三视图.
如图是某几何体的三视图.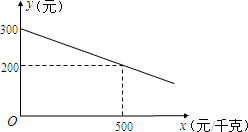 某公司生产一种环保产品,需要添加一种新型原料,若每件产品的利润与新型原料价格成一次函数关系,且每件产品的利润y(元)与新型原料的价格x(元/千克)的函数图象如图:
某公司生产一种环保产品,需要添加一种新型原料,若每件产品的利润与新型原料价格成一次函数关系,且每件产品的利润y(元)与新型原料的价格x(元/千克)的函数图象如图: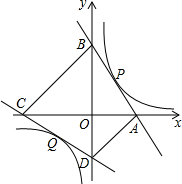 如图,一次函数y=-
如图,一次函数y=-