题目内容
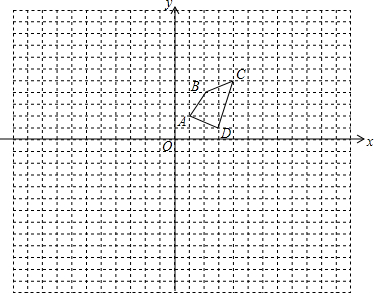
 如图,已知等腰△ABC内接于⊙O,AB=AC=5,BC=8,求点O到BC的距离.
如图,已知等腰△ABC内接于⊙O,AB=AC=5,BC=8,求点O到BC的距离.考点:垂径定理,勾股定理
专题:
分析:连接OA,根据AB=AC得出
=
,再由AO过圆心得出AD垂直并平分BC,根据勾股定理求出AD的长,设OB=r,则OD=r-3,在Rt△BOD中根据勾股定理可得出r的值,进而得出结论.
 |
| AB |
 |
| AC |
解答: 解:连接A0交BC于D,
解:连接A0交BC于D,
∵AB=AC,
∴
=
.
又∵AO过圆心,
∴AD垂直并平分BC,
∴BD=CD=4.
∵AB=5,
∴AD=
=
=3.
设OB=r,则OD=r-3,
在Rt△BOD中,OD2+BD2=OB2,即(r-3)2+42=r2,解得r=
,
∴OD=
-3=
.
 解:连接A0交BC于D,
解:连接A0交BC于D,∵AB=AC,
∴
 |
| AB |
 |
| AC |
又∵AO过圆心,
∴AD垂直并平分BC,
∴BD=CD=4.
∵AB=5,
∴AD=
| AB2-BD2 |
| 52-42 |
设OB=r,则OD=r-3,
在Rt△BOD中,OD2+BD2=OB2,即(r-3)2+42=r2,解得r=
| 25 |
| 6 |
∴OD=
| 25 |
| 6 |
| 7 |
| 6 |
点评:本题考查的是勾股定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
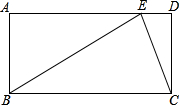 如图,矩形ABCD中,E是AD上一点,BC=BE=2CD,求∠DCE的度数.
如图,矩形ABCD中,E是AD上一点,BC=BE=2CD,求∠DCE的度数.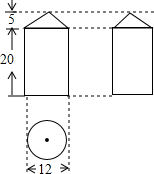 如图是某几何体的三视图.
如图是某几何体的三视图. 如图,A,B,C三点在同一直线上,△ADC,△BEC是等边三角形,连接AE,BD.求证:
如图,A,B,C三点在同一直线上,△ADC,△BEC是等边三角形,连接AE,BD.求证: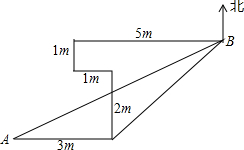 如图,小林在平坦的场地上从A点向东走了3m,再向北走了2m,再向西走了1m,又向北走了1m,最后向东走了5m,到达B点,求A、B之间的距离.
如图,小林在平坦的场地上从A点向东走了3m,再向北走了2m,再向西走了1m,又向北走了1m,最后向东走了5m,到达B点,求A、B之间的距离.