题目内容
(1)问题背景
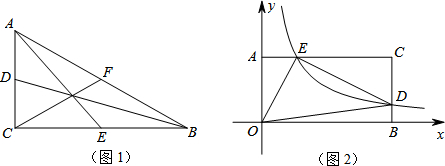
如图①,Rt△ABC中,∠BAC=90°,AB=AC,∠ABC的平分线交直线AC于D,过点C作CE⊥BD,交直线BD于E,CE交直线BA于M.探究线段BD与CE的数量关系得到的结论是 .
(2)类比探索
在(1)中,如果把BD改为△ABC的外角∠ABF的平分线,其他条件均不变(如图②),(1)中的结论还成立吗?若成立,请写出证明过程;若不成立,请说明理由.
(3)拓展延伸
在(2)中,如果AB=
AC,其他条件均不变(如图③),请直接写出BD与CE的数量关系为 .

如图①,Rt△ABC中,∠BAC=90°,AB=AC,∠ABC的平分线交直线AC于D,过点C作CE⊥BD,交直线BD于E,CE交直线BA于M.探究线段BD与CE的数量关系得到的结论是
(2)类比探索
在(1)中,如果把BD改为△ABC的外角∠ABF的平分线,其他条件均不变(如图②),(1)中的结论还成立吗?若成立,请写出证明过程;若不成立,请说明理由.
(3)拓展延伸
在(2)中,如果AB=
| 1 |
| 2 |

考点:全等三角形的判定与性质,等腰直角三角形
专题:
分析:(1)根据角平分线的定义可得∠ABD=∠CBD,再利用“角边角”证明△BME和△BCE全等,根据全等三角形对应边相等可得CE=ME,再求出∠ADB=∠M,然后利用两角的正弦列式整理可得BD=CM,从而得证;
(2)根据角平分线的定义可得∠1=∠2,再根据对顶角相等求出∠3=∠4,然后利用“角边角”证明△BME和△BCE全等,根据全等三角形对应边相等可得CE=ME,再求出∠D=∠M,然后利用两角的正弦列式整理可得BD=CM,从而得证;
(3)根据(2)的求解思路解答即可.
(2)根据角平分线的定义可得∠1=∠2,再根据对顶角相等求出∠3=∠4,然后利用“角边角”证明△BME和△BCE全等,根据全等三角形对应边相等可得CE=ME,再求出∠D=∠M,然后利用两角的正弦列式整理可得BD=CM,从而得证;
(3)根据(2)的求解思路解答即可.
解答:(1)解:∵BE是∠ABC的平分线,
∴∠ABD=∠CBD,
在△BME和△BCE中,
,
∴△BME≌△BCE(ASA),
∴CE=ME,
∵CE⊥BD,∠BAC=90°,
∴∠ABD+∠M=90°,∠ADB+∠ABD=90°,
∴∠ADB=∠M,
∴sin∠ADB=sin∠M,
即
=
,
∵AB=AC,
∴BD=CM,
∴BD=2CE;

(2)结论BD=2CE仍然成立.
证明:∵BD是∠ABF的平分线,
∴∠1=∠2,
∵∠1=∠3,∠2=∠4,
∴∠3=∠4,
在△CBE和△MBE中,
,
∴△CBE≌△MBE(ASA),
∴CE=ME,
∴CM=2CE,
∵∠D+∠DCM=∠M+∠DCM=90°.
∴∠D=∠M,
∴sin∠D=sin∠M,
∴
=
,
∵AB=AC,
∴BD=CM=2CE;
(3)解:同(2)可得
=
,
∵AB=
AC,
∴BD=
CM,
∴BD=CE.
故答案为:(1)BD=2CE;(3)BD=CE.
∴∠ABD=∠CBD,
在△BME和△BCE中,
|
∴△BME≌△BCE(ASA),
∴CE=ME,
∵CE⊥BD,∠BAC=90°,
∴∠ABD+∠M=90°,∠ADB+∠ABD=90°,
∴∠ADB=∠M,
∴sin∠ADB=sin∠M,
即
| AB |
| BD |
| AC |
| CM |
∵AB=AC,
∴BD=CM,
∴BD=2CE;

(2)结论BD=2CE仍然成立.
证明:∵BD是∠ABF的平分线,
∴∠1=∠2,
∵∠1=∠3,∠2=∠4,
∴∠3=∠4,
在△CBE和△MBE中,
|
∴△CBE≌△MBE(ASA),
∴CE=ME,
∴CM=2CE,
∵∠D+∠DCM=∠M+∠DCM=90°.
∴∠D=∠M,
∴sin∠D=sin∠M,
∴
| AB |
| BD |
| AC |
| CM |
∵AB=AC,
∴BD=CM=2CE;
(3)解:同(2)可得
| AB |
| BD |
| AC |
| CM |
∵AB=
| 1 |
| 2 |
∴BD=
| 1 |
| 2 |
∴BD=CE.
故答案为:(1)BD=2CE;(3)BD=CE.
点评:本题考查了全等三角形的判定与性质,等腰直角三角形的性质,锐角三角函数,准确识图判断出全等的三角形是解题的关键利用锐角的正弦列式求解更简便.

练习册系列答案
相关题目
 如图,△ABC是等边三角形,D为BC上的一点,∠BAD=25°,△ABD经过旋转到达△ACE的位置,那么旋转角度为( )
如图,△ABC是等边三角形,D为BC上的一点,∠BAD=25°,△ABD经过旋转到达△ACE的位置,那么旋转角度为( )| A、25° | B、45° |
| C、60° | D、30° |
要使分式
有意义,x的值是( )
| 1 |
| |x|-1 |
| A、x≠1 |
| B、x≠-1 |
| C、-1<x<1 |
| D、x≠1且x≠-1 |
将
-
=1变形为
x=1-
,其错在( )
| x |
| 0.5 |
| 1 |
| 0.7 |
| 10 |
| 5 |
| 10 |
| 7 |
| A、不应将分子、分母同时扩大10倍 |
| B、移项未改变符号 |
| C、1未乘以10 |
| D、以上都不是 |
 如图,AB是⊙O的直径,CB是⊙O的切线,B是切点,OC⊥BD,点E为垂足,若BD=4
如图,AB是⊙O的直径,CB是⊙O的切线,B是切点,OC⊥BD,点E为垂足,若BD=4