题目内容
若二次函数f(x)=ax2+bx+c的对称轴为x=1,且其图象过点(2,0),则
的值是( )
| f(-1) |
| f(1) |
| A、-3 | B、-2 | C、2 | D、3 |
考点:二次函数的性质
专题:
分析:首先根据二次函数的对称性得到图象过点(0,0),将点(0,0)代入f(x)=ax2+bx+c,得c=0,则f(x)=ax2+bx.再由对称轴为x=1,得出b=-2a,
然后将x=-1代入f(x)=ax2+bx,求出f(-1)=3a,同样求出f(1)=-a,则
=
=-3.
然后将x=-1代入f(x)=ax2+bx,求出f(-1)=3a,同样求出f(1)=-a,则
| f(-1) |
| f(1) |
| 3a |
| -a |
解答:解:∵二次函数f(x)=ax2+bx+c的对称轴为x=1,且其图象过点(2,0),
∴图象过点(0,0),
将点(0,0)代入f(x)=ax2+bx+c,得c=0,
∴f(x)=ax2+bx.
∵对称轴为x=1,
∴
=1,
∴b=-2a.
∵f(-1)=a-b=a-(-2a)=3a,f(1)=a+b=a+(-2a)=-a,
∴
=
=-3.
故选A.
∴图象过点(0,0),
将点(0,0)代入f(x)=ax2+bx+c,得c=0,
∴f(x)=ax2+bx.
∵对称轴为x=1,
∴
| -b |
| 2a |
∴b=-2a.
∵f(-1)=a-b=a-(-2a)=3a,f(1)=a+b=a+(-2a)=-a,
∴
| f(-1) |
| f(1) |
| 3a |
| -a |
故选A.
点评:本题考查了二次函数的性质,二次函数图象上点的坐标特征,根据对称性得到图象过点(0,0)是解题的关键.

练习册系列答案
相关题目
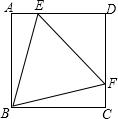 如图,正方形ABCD中,AB=4,点E,F分别在AD,DC上,且△BEF为等边三角形,则△EDF与△BFC的面积比为( )
如图,正方形ABCD中,AB=4,点E,F分别在AD,DC上,且△BEF为等边三角形,则△EDF与△BFC的面积比为( )| A、2:1 | B、3:1 |
| C、3:2 | D、5:3 |
小刘用84米长的铁丝围成一个长方形,要使长比宽多4米,则长方形的长为( )
| A、29 | B、27 | C、25 | D、23 |
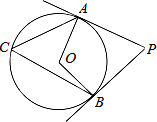 如图,AP、BP分别切⊙O于点A、B,∠P=60°,点C是圆上一动点,则∠C的度数为( )
如图,AP、BP分别切⊙O于点A、B,∠P=60°,点C是圆上一动点,则∠C的度数为( )| A、60 | B、40 |
| C、72° | D、60°或120° |
 如图,△ABC是等边三角形,D为BC上的一点,∠BAD=25°,△ABD经过旋转到达△ACE的位置,那么旋转角度为( )
如图,△ABC是等边三角形,D为BC上的一点,∠BAD=25°,△ABD经过旋转到达△ACE的位置,那么旋转角度为( )| A、25° | B、45° |
| C、60° | D、30° |
要使分式
有意义,x的值是( )
| 1 |
| |x|-1 |
| A、x≠1 |
| B、x≠-1 |
| C、-1<x<1 |
| D、x≠1且x≠-1 |
 如图,AB是⊙O的直径,CB是⊙O的切线,B是切点,OC⊥BD,点E为垂足,若BD=4
如图,AB是⊙O的直径,CB是⊙O的切线,B是切点,OC⊥BD,点E为垂足,若BD=4