题目内容
(1)已知关于x的一元二次方程(x-m)2+6x=4m-3有实数根.试求m的取值范围;
(2)我校为了学生积极参加体育活动,决定再购进一定数量的体育器材,器材管理员对购买的部分器材进行了统计,图1和图2是器材管理员通过采集数据后,绘制的两幅不完整的频率分布表与频数分布直方图.请你根据图表中提供的信息,解答以下问题:
(1)填充图1频率分布表中的空格.
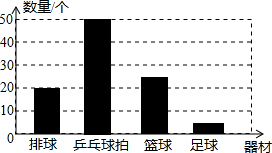
(2)在图2中,将表示“排球”和“足球”的部分补充完整.
(3)若该管理员购买这批体育器材时,篮球和足球一共花去950元,且足球每个的价格比篮球多10元,试求出篮球与足球的单价各位多少元?
图1,频数分布表
图2,
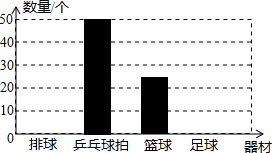
(2)我校为了学生积极参加体育活动,决定再购进一定数量的体育器材,器材管理员对购买的部分器材进行了统计,图1和图2是器材管理员通过采集数据后,绘制的两幅不完整的频率分布表与频数分布直方图.请你根据图表中提供的信息,解答以下问题:
(1)填充图1频率分布表中的空格.
(2)在图2中,将表示“排球”和“足球”的部分补充完整.
(3)若该管理员购买这批体育器材时,篮球和足球一共花去950元,且足球每个的价格比篮球多10元,试求出篮球与足球的单价各位多少元?
图1,频数分布表
| 器材种类 | 频数 | 频率 |
| 排球 | 20 | |
| 乒乓球拍 | 50 | 0.50 |
| 篮球 | 25 | 0.25 |
| 足球 | ||
| 合计 | 1 |

考点:频数(率)分布表,根的判别式,条形统计图
专题:计算题
分析:(1)先把方程整理为一般式,再根据判别式的意义得到4(m-3)2-4(m2-4m+3)≥0,然后解不等式即可;
(2)先利用乒乓球的数量和频率计算出购进体育器材的总数量,再用排球的数量除以总数量得到排球的频率,然后用总数量分别减去排球、乒乓球和篮球的数量即可得到足球的数量,再计算足球的频率;
(3)设每个篮球的价格为x元,则每个足球的价格为(x+10)元,根据25个篮球和5个足球的总价格为950元得到25x+5(x+10)=950,然后解方程解得x=30,再计算x+10.
(2)先利用乒乓球的数量和频率计算出购进体育器材的总数量,再用排球的数量除以总数量得到排球的频率,然后用总数量分别减去排球、乒乓球和篮球的数量即可得到足球的数量,再计算足球的频率;
(3)设每个篮球的价格为x元,则每个足球的价格为(x+10)元,根据25个篮球和5个足球的总价格为950元得到25x+5(x+10)=950,然后解方程解得x=30,再计算x+10.
解答:解:(1)方程整理为x2-2(m-3)x+m2-4m+3=0,
根据题意得△=4(m-3)2-4(m2-4m+3)≥0,
解得m≤3;
(2)①购进体育器材的总数量=50÷0.5=100,
排球的频率=
=0.2,
足球的数量=100-20-50-25=5,足球的频率=
=0.05,
填表如下:
故答案为0.2,5,0.05,100;
②如图所示:
③设每个篮球的价格为x元,则每个足球的价格为(x+10)元,
根据题意得25x+5(x+10)=950,
解得x=30,
所以x+10=40.
答:每个篮球和足球的价格分别为30元和40元.
根据题意得△=4(m-3)2-4(m2-4m+3)≥0,
解得m≤3;
(2)①购进体育器材的总数量=50÷0.5=100,
排球的频率=
| 20 |
| 100 |
足球的数量=100-20-50-25=5,足球的频率=
| 5 |
| 100 |
填表如下:
| 器材种类 | 频数 | 频率 |
| 排球 | 20 | 0.2 |
| 乒乓球拍 | 50 | 0.50 |
| 篮球 | 25 | 0.25 |
| 足球 | 5 | 0.05 |
| 合计 | 100 | 1 |
②如图所示:

③设每个篮球的价格为x元,则每个足球的价格为(x+10)元,
根据题意得25x+5(x+10)=950,
解得x=30,
所以x+10=40.
答:每个篮球和足球的价格分别为30元和40元.
点评:本题考查了频数(率)分布表:在统计数据时,经常把数据按照不同的范围分成几个组,分成的组的个数称为组数,每一组两个端点的差称为组距,称这样画出的统计图表为频数分布表.也考查了根的判别式和一元一次方程的应用.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
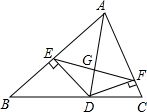 已知:如图,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别是E,F,EF交AD于点G.
已知:如图,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别是E,F,EF交AD于点G.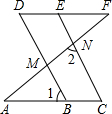 如图,已知DF∥AC,∠C=∠D,要证∠AMB=∠2,请完善证明过程:
如图,已知DF∥AC,∠C=∠D,要证∠AMB=∠2,请完善证明过程: 在图中,这些方砖除颜色外完全相同,小老鼠在方砖上自由走动,最终停在白色方砖上的概率为
在图中,这些方砖除颜色外完全相同,小老鼠在方砖上自由走动,最终停在白色方砖上的概率为