题目内容
解下列不等式（组）：
（1）1+
＞5-
；
（2）
．
（1）1+
| x |
| 3 |
| x-3 |
| 6 |
（2）
|
考点：解一元一次不等式组,解一元一次不等式
专题：
分析：（1）先去分母，再去括号，移项、合并同类项，把x的系数化为1即可；
（2）分别求出各不等式的解集，再求出其公共解集即可．
（2）分别求出各不等式的解集，再求出其公共解集即可．
解答：解：（1）去分母得，6+2x＞30-（x-3），
去括号得，6+2x＞30-x+3，
移项得，2x+x＞30-3-6，
合并同类项得，3x＞21，
把x的系数化为1得，x＞7；
（2）
，
由①得，x＜1，
由②得，x＜-3，
故此不等式组的解集为；x＜-3．
去括号得，6+2x＞30-x+3，
移项得，2x+x＞30-3-6，
合并同类项得，3x＞21，
把x的系数化为1得，x＞7；
（2）
|
由①得，x＜1，
由②得，x＜-3，
故此不等式组的解集为；x＜-3．
点评：本题考查的是解一元一次不等式组，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的法则是解答此题的关键．
练习册系列答案
优生乐园系列答案
新编小学单元自测题系列答案
相关题目
为求1+2+22+23+…+22008的值，可令S=1+2+22+23+…+22008，则2S=2+22+23+24+…+22009，因此2S-S=22009-1，所以1+2+22+23+…+22008=22009-1．仿照以上推理计算出1+3+32+33+…+32014的值是（ ）
| A、32015-1 | ||
| B、32014-1 | ||
C、
| ||
D、
|
如图，直线l与坐标轴分别交于A、B两点，∠BAO=45°，点A坐标为（8，0）．动点P从点O出发，沿折线段OBA运动，到点A停止；同时动点Q也从点O出发，沿线段OA运动，到点A停止；它们的运动速度均为每秒1个单位长度．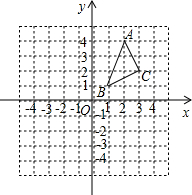
△ABC在平面直角坐标系中的位置如图．A、B、C三点在格点上．
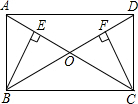如图，矩形ABCD中，AC与BD交于点O，BE⊥AC于E，CF⊥BD于F．