题目内容
7.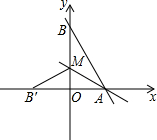 如图,直线y=-$\frac{4}{3}$x+8与x轴,y轴分别交于点A和B,M是OB上的一点,若将△ABM沿AM折叠,点B恰好落在x轴上的点B′处,则△AMO的面积为9.
如图,直线y=-$\frac{4}{3}$x+8与x轴,y轴分别交于点A和B,M是OB上的一点,若将△ABM沿AM折叠,点B恰好落在x轴上的点B′处,则△AMO的面积为9.
分析 由题意,可求得点A与B的坐标,由勾股定理,可求得AB的值,又由折叠的性质,可求得AB′与OB′的长,BM=B′M,然后设MO=x,由在Rt△OMB′中,OM2+OB′2=B′M2,求出x的值,进而求出△AMO的面积.
解答 解:令y=0得x=6,令x=0得y=8,
∴点A的坐标为:(6,0),点B坐标为:(0,8),
∵∠AOB=90°,
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=10,
由折叠的性质,得:AB=AB′=10,
∴OB′=AB′-OA=10-6=4,
设MO=x,则MB=MB′=8-x,
在Rt△OMB′中,OM2+OB′2=B′M2,
即x2+42=(8-x)2,
解得:x=3,
S△AMO=$\frac{1}{2}$OM•OA=$\frac{1}{2}$×3×6=9.
故答案为9.
点评 此题考查了折叠的性质、一次函数图象上点的坐标特征、勾股定理等知识,解答本题的关键是求出OM的长度,此题难度适中,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
相关题目
20. 如图所示,已知AB∥CD,AD∥BC,那么图中共有全等三角形( )
如图所示,已知AB∥CD,AD∥BC,那么图中共有全等三角形( )
 如图所示,已知AB∥CD,AD∥BC,那么图中共有全等三角形( )
如图所示,已知AB∥CD,AD∥BC,那么图中共有全等三角形( )| A. | 1对 | B. | 2对 | C. | 4对 | D. | 8对 |

 每天早上小明爸爸送他上学,都会看到远处一个巨大的广告牌,小明想知道广告牌离地面有多高,于是特意测量了一下,发现A出观察广告牌底端C的仰角是20°,在B处观察广告牌底端C的仰角是53°,爸爸告诉小明刚才的车速是42千米/时,从A到B用了3秒钟,请你帮小明算一下广告牌底端离地面有多高?(温馨提示:sin53°≈$\frac{4}{5}$,cos53°≈$\frac{4}{3}$,sin20°≈$\frac{3}{10}$,cos20°≈$\frac{9}{10}$,tan20°≈$\frac{2}{5}$)
每天早上小明爸爸送他上学,都会看到远处一个巨大的广告牌,小明想知道广告牌离地面有多高,于是特意测量了一下,发现A出观察广告牌底端C的仰角是20°,在B处观察广告牌底端C的仰角是53°,爸爸告诉小明刚才的车速是42千米/时,从A到B用了3秒钟,请你帮小明算一下广告牌底端离地面有多高?(温馨提示:sin53°≈$\frac{4}{5}$,cos53°≈$\frac{4}{3}$,sin20°≈$\frac{3}{10}$,cos20°≈$\frac{9}{10}$,tan20°≈$\frac{2}{5}$)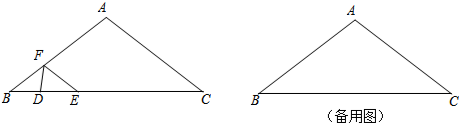
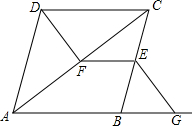 如图,在菱形ABCD中,E、F分别是BC、AC上的点,G是AB延长线上的一点,且EF∥CD,∠BEG=∠CDF,求证:DF=EG.
如图,在菱形ABCD中,E、F分别是BC、AC上的点,G是AB延长线上的一点,且EF∥CD,∠BEG=∠CDF,求证:DF=EG.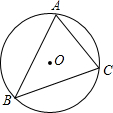 如图,已知△ABC的外接圆O的半径为3,AC=4,则sinB=$\frac{2}{3}$.
如图,已知△ABC的外接圆O的半径为3,AC=4,则sinB=$\frac{2}{3}$.